Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vậy \(S=4\pi r^2=4\pi\left(\dfrac{a\sqrt{2}}{2}\right)^2=2\pi a^2\) và \(V=\dfrac{4}{3}\pi r^3=\dfrac{4}{3}\pi\left(\dfrac{a\sqrt{2}}{2}\right)^3=\dfrac{1}{3}\pi a^3\sqrt{2}\)

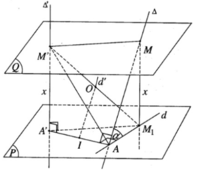
Hình tứ giác A’M’M M 1 là hình chữ nhật nên tâm O cũng là trung điểm của A’M. Do đó khi x thay đổi thì mặt phẳng (Q) thay đổi và điểm O luôn luôn thuộc đường thẳng d’ đi qua trung điểm I của đoạn AA’ và song song với đường thẳng ∆ . Vì mặt cầu tâm O luôn luôn đi qua hai điểm cố định A, A’nên nó có tâm O di động trên đường thẳng d’. Do đó mặt cầu tâm O luôn luôn chứa đường tròn tâm I cố định có đường kính AA’ cố định và nằm trong mặt phẳng cố định vuông góc với đường thẳng d’.











Đáp án C
Cách giải:
M di động luôn nhìn đoạn AB dưới một góc vuông ⇒ M thuộc mặt cầu có một đường kính là AB.