tìm x : x^3-5x^2-9x+45=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


x3 - 9x - 5x2 + 45 = 0
⇔ ( x3 - 5x2 ) - ( 9x - 45 ) = 0
⇔ x2( x - 5 ) - 9( x - 5 ) = 0
⇔ ( x - 5 )( x2 - 9 ) = 0
⇔ ( x - 5 )( x - 3 )( x + 3 ) = 0
⇔ x - 5 = 0 hoặc x - 3 = 0 hoặc x + 3 = 0
⇔ x = 5 hoặc x = ±3
\(x^3-9x-5x^2+45=0\)
\(x^3-5x^2-9x+45=0\)
\(x^2\left(x-5\right)-9\left(x-5\right)=0\)
\(\left(x-5\right)\left(x^2-9\right)=0\)
\(\orbr{\begin{cases}x-5=0\\x^2-9=0\end{cases}}\)
\(\orbr{\begin{cases}x=5\\x=\pm3\end{cases}}\)

\(x^3+6x^2+9x=0\)
\(x\left(x^2+6x+9\right)=0\)
\(x\left(x+3\right)^2=0\)
\(\Rightarrow\hept{\begin{cases}x=0\\x=-3\end{cases}}\)

d) \(4x^2-9-x\left(2x-3\right)=0\)
\(\Leftrightarrow4x^2-9-2x^2+3x=0\)
\(\Leftrightarrow2x^2+3x-9=0\)
\(\Delta=3^2-4.2.\left(-9\right)=9+72=81\)
Vậy pt có 2 nghiệm phân biệt
\(x_1=\frac{-3+\sqrt{81}}{4}=\frac{-3}{2}\);\(x_1=\frac{-3-\sqrt{81}}{4}=-3\)
e) \(x^3+5x^2+9x=-45\)
\(\Leftrightarrow x^3+5x^2+9x+45=0\)
\(\Leftrightarrow x^2\left(x+5\right)+9\left(x+5\right)=0\)
\(\Leftrightarrow\left(x^2+9\right)\left(x+5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+9=0\\x+5=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\pm3i\\x=-5\end{cases}}\)

Ta có: \(x^3+5x^2+9x+45=0\)
\(\Leftrightarrow x^2\left(x+5\right)+9\left(x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(x^2+9\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+5=0\\x^2+9=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-5\\x\in\varnothing\end{cases}}\)\(\Leftrightarrow x=-5\)
k mình nha bn thanks nhìu

d: Ta có: \(9x^2+6x-8=0\)
\(\Leftrightarrow9x^2+12x-6x-8=0\)
\(\Leftrightarrow\left(3x+4\right)\left(3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{4}{3}\\x=\dfrac{2}{3}\end{matrix}\right.\)
e: Ta có: \(x\left(x-2\right)+x-2=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
f: Ta có: \(5x\left(x-3\right)-x+3=0\)
\(\Leftrightarrow\left(x-3\right)\left(5x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{5}\end{matrix}\right.\)

a)\(7x\left(x-2\right)=\left(x-2\right)\)
\(\Leftrightarrow7x\left(x-2\right)-\left(x-2\right)=0\)
\(\Leftrightarrow\left(7x-1\right)\left(x-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}7x-1=0\\x-2=0\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{7}\\x=2\end{matrix}\right.\)
b)\(4x^2-9-x\left(2x-3\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(2x+3\right)-x\left(2x-3\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(2x+3-x\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(x+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2x-3=0\\x+3=0\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-3\end{matrix}\right.\)
c)\(x^3+5x^2+9x=-45\)
\(\Leftrightarrow x^3+9x+5x^2+45=0\)
\(\Leftrightarrow x\left(x^2+9\right)+5\left(x^2+9\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(x^2+9\right)=0\)
Dễ thấy: \(x^2+9\ge 9 >0\forall x\)
\(\Rightarrow x+5=0\Rightarrow x=-5\)
d,e tương tự

1) \(x^3+5x^2+9x=-45\)
\(\Rightarrow x^2\left(x+5\right)+9x+45=0\)
\(\Rightarrow x^2\left(x+5\right)+9\left(x+5\right)=0\)
\(\Rightarrow\left(x^2+9\right)\left(x+5\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x^2+9=0\\x+5=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x^2=-9\left(loai\right)\\x=-5\left(nhan\right)\end{cases}}\)
2) \(x^3-6x^2-x+30=0\)
\(\Rightarrow x^3-3x^2-3x^2+9x-10x+30=0\)
\(\Rightarrow x^2\left(x-3\right)-3x\left(x-3\right)-10\left(x-3\right)=0\)
\(\Rightarrow\left(x^2-3x-10\right)\left(x-3\right)=0\)
\(\Rightarrow\left(x^2-5x+2x-10\right)\left(x-3\right)=0\)
\(\Rightarrow\left[x\left(x-5\right)+2\left(x-5\right)\right]\left(x-3\right)=0\)
\(\Rightarrow\left(x+2\right)\left(x-3\right)\left(x-5\right)=0\)
\(\)Từ đây giải x giống câu trên nhé.
3) \(x^2+16=10x\)
\(\Rightarrow x^2-10x+16=0\)
\(\Rightarrow\left(x-8\right)\left(x-2\right)=0\)
Tương tự....

b: \(B=\dfrac{x^2-3x+2x^2+6x-3x^2-9}{x^2-9}=\dfrac{3x-9}{\left(x-3\right)\left(x+3\right)}=\dfrac{3}{x+3}\)
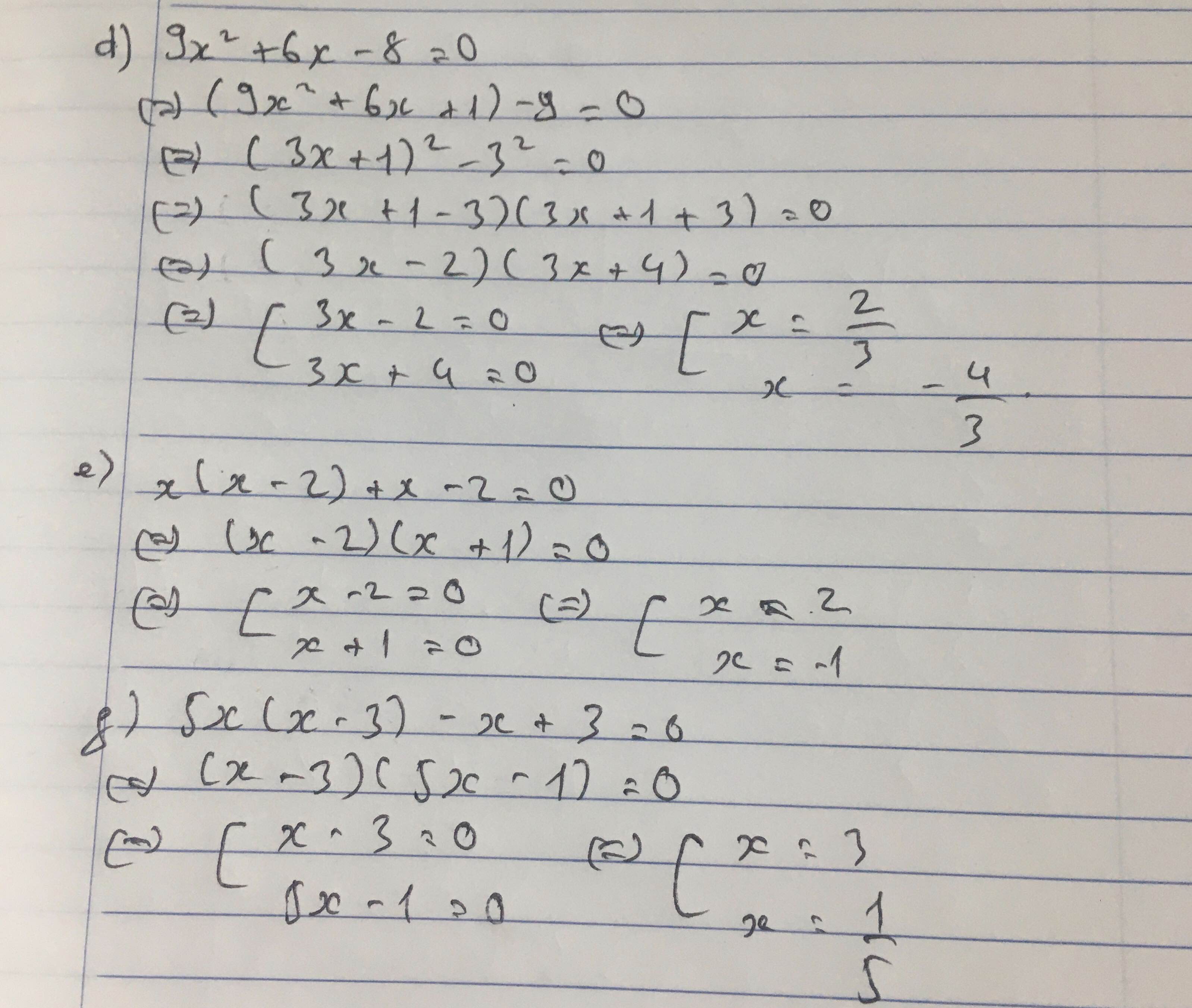 Mình trình bày trong hình ^^ Bn tham khảo nhé
Mình trình bày trong hình ^^ Bn tham khảo nhé
x^3-5x^2-9x+45=0
=> x^3 + 3x^2 - 8x^2 - 24x + 15x + 45 = 0
=> x^2(x + 3) - 8x(x + 3) + 15(x + 3) = 0
=> (x^2 - 8x + 15)(x + 3) = 0
=> (x - 3)(x - 5)(x + 3) = 0
=> x = 3 hoặc x = 5 hoặc x = -3
x^3-5x^2-9x+45=0
(x^3-5x^2)-(9x-45)=0
x^2(x-5)-9(x-5)=0
(x-5)(x^2-9)=0
(x-5)(x+3)(x-3)=0
x-5=0 hoặc x+3=0 hoặc x-3=0
x=5 x=-3 x=3