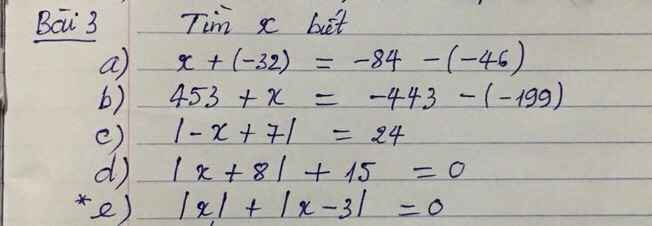
giúp mik câu c, d, e vớiiiiiiiiiiiiiiiiiiii
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
giúp em vớiiiiiiiiiiiiiiiiiiii
H9
HT.Phong (9A5)
CTVHS
7 tháng 9 2023
6) Ta có: \(\widehat{xOy}\) và \(\widehat{yOz}\) là 2 góc kề bù nên:
\(\widehat{xOy}+\widehat{yOz}=180^o\)
\(\Rightarrow\widehat{yOz}=180^o-80^o=100^o\)
Mà: Om là tia phân giác của \(\widehat{xOy}\) nên:
\(\widehat{xOm}=\widehat{mOy}\)
\(\Rightarrow\widehat{mOy}=\dfrac{\widehat{xOy}}{2}=\dfrac{80^o}{2}=40^o\)
On là tia phân giác của \(\widehat{yOz}\) nên:
\(\widehat{yOn}=\widehat{nOy}\)
\(\Rightarrow\widehat{nOy}=\dfrac{\widehat{yOz}}{2}=\dfrac{100^o}{2}=50^o\)
Mà: \(\widehat{mOn}=\widehat{mOy}+\widehat{nOy}\)
\(\Rightarrow\widehat{mOn}=50^o+40^o=90^o\)
3 tháng 10 2021
\(c,\Rightarrow\left|x-\dfrac{1}{9}\right|=-\dfrac{4}{5}\\ \Rightarrow x\in\varnothing\left(\left|x-\dfrac{1}{9}\right|\ge0>-\dfrac{4}{5}\right)\\ d,\Rightarrow\left\{{}\begin{matrix}3x-2=0\\4y-7=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{7}{4}\end{matrix}\right.\\ e,\Rightarrow\left\{{}\begin{matrix}2x+1=0\\x-y=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\x=y=-\dfrac{1}{2}\end{matrix}\right.\Rightarrow x=y=-\dfrac{1}{2}\)
giúp mik câu c d e f thôi ạ :))
2 tháng 10 2021
a: \(\left(x-1.2\right)^2=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1.2=2\\x-1.2=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3.2\\x=-0.8\end{matrix}\right.\)
b: Ta có: \(\left(x+1\right)^3=-125\)
\(\Leftrightarrow x+1=-5\)
hay x=-6
DT
10 tháng 4 2023
Để phương trình có 2 nghiệm phân biệt thì:
\(\Delta>0\\ \Leftrightarrow\left(-5\right)^2-4.1.\left(m+4\right)>0\\ \Leftrightarrow25-4m-16>0\\\Leftrightarrow9-4m>0\\ \Leftrightarrow m< \dfrac{9}{4}\)
Theo viét:
\(\left\{{}\begin{matrix}x_1+x_2=5\\x_1x_2=m+4\end{matrix}\right.\)
c,
\(\left|x_1-x_2\right|=3\\ \Leftrightarrow\left(x_1-x_2\right)^2=9\\ \Leftrightarrow x_1^2-2x_1x_2+x_2^2=9\\ \Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=9\\ \Leftrightarrow5^2-4\left(m+4\right)=9\\ \Leftrightarrow25-4m-16=9\\ \Leftrightarrow m=0\left(nhận\right)\)
d.
\(\left|x_1\right|+\left|x_2\right|=4\\ \)
Xét trường hợp 1: hai nghiệm đều dương:
ta có:
\(x_1+x_2=4\)
5 = 4 (vô lý)
Loại trường hợp này.
Xét trường hợp 2: hai nghiệm đều âm, tương tự ta loại trường hợp này.
Xét trường hợp 3:
\(x_1< 0< x_2\)
=> \(x_2-x_1=4\)
<=> \(x_2+x_1-2x_1=4\)
=> \(5-2x_1=4\)
=> \(x_1=\dfrac{1}{2}\)
\(x_2< 0< x_1\)
\(x_1-x_2=4\\ \Leftrightarrow x_1+x_2-2x_2=4\\ \Leftrightarrow5-2x_2=4\\ \Rightarrow x_2=\dfrac{1}{2}\)
Có: \(x_1x_2=m+4\\\)
<=> \(\dfrac{1}{2}.\dfrac{1}{2}=m+4\)
=> m = -3,75 (nhận)
e.
Theo viét và theo đề ta có:
\(\left\{{}\begin{matrix}3x_1+4x_2=6\left(1\right)\\x_1+x_2=5\left(2\right)\\x_1x_2=m+4\left(3\right)\end{matrix}\right.\)
Từ (1) có \(x_1=\dfrac{6-4x_2}{3}=2-\dfrac{4}{3}x_2\) (x)
Thế (x) vào (2) được \(2-\dfrac{4}{3}x_2+x_2=5\)
=> \(x_2=-9\) (xx)
Thế (xx) vào (1) được \(3x_1+4.\left(-9\right)=6\)
=> \(x_1=14\) (xxx)
Thế (xx) và (xxx) vào (3) được:
\(14.\left(-9\right)=m+4\)
=> m = -130 (nhận)
h.
\(x_1\left(1-3x_2\right)+x_2\left(1-3x_1\right)=m^2-23\)
<=> \(x_1-3x_1x_2+x_2-3x_1x_2=m^2-23\)
<=> \(x_1+x_2-6x_1x_2=m^2-23\)
<=> \(5-6.\left(m+4\right)=m^2-23\)
<=> \(5-6m-20-m^2+23=0\)
<=> \(-m^2-6m+8=0\)
\(\Delta=\left(-6\right)^2-4.\left(-1\right).8=68\)
\(m_1=\dfrac{6+\sqrt{68}}{2.\left(-1\right)}=-3-\sqrt{17}\left(nhận\right)\)
\(m_2=\dfrac{6-\sqrt{68}}{2.\left(-1\right)}=-3+\sqrt{17}\left(nhận\right)\)
☕T.Lam
Mình không chắc chắn ở câu d, mình lên đây để ôn bài thi tiện thể giúp được bạn phần nào.
CM
Cô Mỹ Linh
Manager
22 tháng 12 2022
Em đưa cả ngữ liệu và đề bài đầy đủ lên đây để thầy cô và các bạn trong cộng đồng có thể hỗ trợ nhé!
DT
3
G
8 tháng 8 2023
d) \(y=4sinx-2cos2x-1\)
\(=4sinx-2\left(1-2sin^2x\right)-1\)
\(=4sin^2x+4sinx-3\)
Đặt \(t=sinx,t\in\left[-1;1\right]\)
\(y=f\left(t\right)=4t^2+4t-3\) \(\Leftrightarrow f'\left(t\right)=8t+4\)
\(f'\left(t\right)=0\Leftrightarrow t=-\dfrac{1}{2}\)
Vẽ BBT với \(t\in\left[-1;1\right]\) ta được
\(minf\left(t\right)=miny=-4\Leftrightarrow t=-\dfrac{1}{2}\)\(\Leftrightarrow sinx=-\dfrac{1}{2}\)\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{6}+k2\pi\\x=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\) ( k thuộc Z)
\(maxf\left(t\right)=miny=5\Leftrightarrow t=1\)\(\Leftrightarrow sinx=1\) \(\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\) ( k thuộc Z)
Vậy...
G
8 tháng 8 2023
e) \(y=3sin2x+8cos^2x-1\)
\(=3sin2x+4\left(2cos^2x-1\right)+3\)
\(=3sin2x+4cos2x+3\)
\(=5\left(\dfrac{3}{5}sin2x+\dfrac{4}{5}cos2x\right)+3\)
Đặt \(cosu=\dfrac{3}{5}\Leftrightarrow sinu=\dfrac{4}{5}\)
\(y=5\left(sin2x.cosu+cos2x.sinu\right)+3=5.sin\left(2x+u\right)+3\)
Có \(-1\le sin\left(2x+u\right)\le1\) \(\Leftrightarrow-2\le y\le8\)
\(maxy=8\Leftrightarrow sin\left(2x+u\right)=1\) \(\Leftrightarrow2x+u=\dfrac{\pi}{2}+k2\pi\) \(\Leftrightarrow x=-\dfrac{u}{2}+\dfrac{\pi}{4}+k\pi\)\(\Leftrightarrow x=-\dfrac{1}{2}.arccos\dfrac{3}{5}+\dfrac{\pi}{4}+k\pi\) ( k thuộc Z)
\(miny=-2\Leftrightarrow sin\left(2x+u\right)=-1\)\(\Leftrightarrow x=-\dfrac{1}{2}.\dfrac{arccos3}{5}-\dfrac{\pi}{4}+k\pi\) ( k thuộc Z)
Vậy...
c) |-x+7|=24
⇒\(\left[{}\begin{matrix}-x+7=24\\-x+7=-24\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-17\\x=31\end{matrix}\right.\)
d) |x+8|+15=0
|x+8|=0-15
|x+8|=-15
⇒x=∅
e) |x|+|x-3|=0
\(\Rightarrow\left[{}\begin{matrix}x=0\\x-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
c: Ta có: \(\left|-x+7\right|=24\)
\(\Leftrightarrow\left[{}\begin{matrix}7-x=24\\7-x=-24\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-17\\x=31\end{matrix}\right.\)