
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
x y m B A C 1 1 2 1
Qua B, vẽ tia Bm sao cho Bm // Ax
Bm // Ax ( cách vẽ ) => góc A1 + góc B1 = 180o ( trong cùng phía )
Mà góc A1 = 140o ( giả thiết ) => góc B1 = 40o
Ta có: góc B1 + góc B2 = góc ABC
Mà góc ABC = 70o ( giả thiết ); góc B1 = 40o ( chứng minh trên )
=> góc B2 = 30o
Ta có: góc B2 + góc C1 = 30o + 150o = 180o
Mà hai góc này ở vị trí trong cùng phía
=> Bm // Cy ( dấu hiệu nhận biết 2 đường thẳng song song )
Ta lại có:
Ax // Bm ( cách vẽ ); Cy // Bm ( chứng minh trên )
=> Ax // Cy ( tính chất 3 quan hệ từ vuông góc đến song song ) ( đpcm )
Bài 3:
A B C F E G N M H 1 2
a) Chứng minh AH < \(\dfrac{1}{2}\) ( AB + AC )
+) Vì AH vuông góc với BC ( giả thiết )
=> AH < AB ( quan hệ giữa đường vuông góc và đường xiên ) ( 1 )
+) Vì AH vuông góc với BC ( giả thiết )
=> AH < AC ( quan hệ giữa đường vuông góc và đường xiên ) ( 2 )
+) Từ ( 1 ) và ( 2 ) => AH + AH < AB + AC
=> 2 . AH < AB + AC
=> AH < \(\dfrac{1}{2}\) ( AB + AC ) ( đpcm )
b) Chứng minh EF = BC
+) Vì BM là đường trung tuyến của tam giác ABC ( giả thiết )
=> \(\dfrac{BG}{BM}=\dfrac{2}{3}\)
=> \(\dfrac{MG}{BG}=\dfrac{1}{2}\)
=> 2 . MG = BG
Mà EM = MG ( do BM là đường trung tuyến của tam giác ABC )
=> EM + MG = BG => EG = BG
+) Vì CN là đường trung tuyến của tam giác ABC ( giả thiết )
=> \(\dfrac{CG}{CN}=\dfrac{2}{3}\)
=> \(\dfrac{GN}{CG}=\dfrac{1}{2}\)
=> 2 . GN = CG
Mà FN = GN ( do CN là đường trung tuyến của tam giác ABC )
=> FN + GN = CG => FG = CG
Góc G1 = góc G2 ( đối đỉnh )
Xét tam giác FEG và tam giác CBG có:
FG = CG ( chứng minh trên )
EG = BG ( chứng minh trên )
Góc G1 = góc G2 ( chứng minh trên )
=> tam giác FEG = tam giác CBG ( c.g.c )
=> EF = BC ( 2 cạnh tương ứng ) ( đpcm )


Câu 7:
Giải:
Giá tiền của mỗi chiếc máy tính bán trong đợt đầu là:
8 x (100% + 30%) = 10,4(triệu đồng)
Tổng số tiền thu được khi bán 70 chiếc máy tính trong đợt đầu là:
10,4 x 70 = 728 (triệu đồng)
Giá của mỗi chiếc máy tính bán được trong đợt sau là:
10,4 x 65% = 6,76(triệu đồng)
Số tiền thu được khi bán hết số máy tính còn lại là:
6,76 x (100 - 70) = 202,8 (triệu đồng)
Tổng số tiền mà cửa hàng thu được khi bán hết 100 cái máy tính là:
728 + 202,8 = 930,8 (triệu đồng)
Tiền vốn của 100 cái máy tính là:
8 x 100 = 800 (triệu đồng)
Sau khi bán hết 100 máy tính thì người đó lãi và lãi số tiền là:
930,8 - 800 = 130,8 (triệu đồng)
Kết luận: Sau khi bán hết 100 máy tính người đó lãi và lãi số tiền là 130,8 triệu đồng
Bài 8:
a; Doanh thu năm 2019 là: 5,6 x \(\frac34\) = 4,2 (triệu usd)
b; Sau năm năm để lời 7,8 triệu usd thì năm 2020 phải thu được:
7,8 - (-1,8 + 5,6 - 3,6 + 4,2) = 3,4(triệu usd)
Kết luận: năm 2019 thu 4,2 triệu usd
năm 2020 thu 3,4 triệu usd


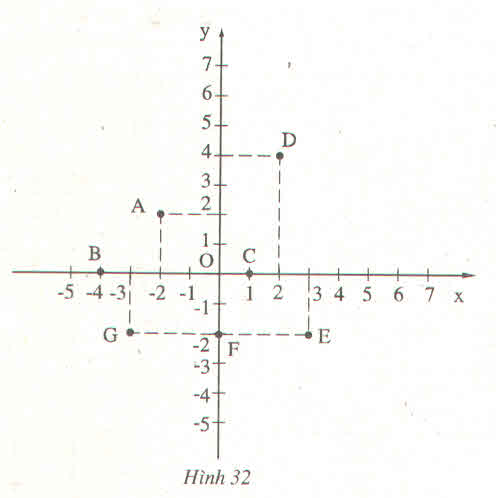
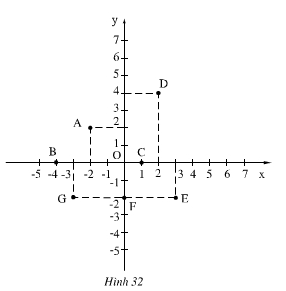
Ta có tọa độ các điểm: A(-2; 2); B(-4; 0); C(1; 0); D(2; 4); E(3; -2); F(0; -2); G(-3; -2)

a: Ta có: \(\hat{AOD}+\hat{BOD}=180^0\) (hai góc kề bù)
=>\(\hat{BOD}=180^0-97^0=83^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OA, ta có: \(\hat{AOE}<\hat{AOD}\left(56^0<97^0\right)\)
nên tia OE nằm giữa hai tia OA và OD
=>\(\hat{AOE}+\hat{EOD}=\hat{AOD}\)
=>\(\hat{EOD}=97^0-56^0=41^0\)
Ta có: \(\hat{AOE}+\hat{EOC}+\hat{COB}=180^0\)
=>\(\hat{EOC}=180^0-56^0-42^0=82^0\)
b: Trên cùng một nửa mặt phẳng bờ chứa tia OE, ta có; \(\hat{EOD}<\hat{EOC}\left(41^0<82^0\right)\)
nên tia OD nằm giữa hai tia OE và OC
=>\(\hat{EOD}+\hat{DOC}=\hat{EOC}\)
=>\(\hat{DOC}=82^0-41^0=41^0\)
Ta có: tia OD nằm giữa hai tia OE và OC
\(\hat{DOE}=\hat{DOC}\left(=41^0\right)\)
Do đó: OD là phân giác của góc EOC











 d với nha, mik đag cần gấp.
d với nha, mik đag cần gấp.
\(c,\Rightarrow\left|x-\dfrac{1}{9}\right|=-\dfrac{4}{5}\\ \Rightarrow x\in\varnothing\left(\left|x-\dfrac{1}{9}\right|\ge0>-\dfrac{4}{5}\right)\\ d,\Rightarrow\left\{{}\begin{matrix}3x-2=0\\4y-7=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{7}{4}\end{matrix}\right.\\ e,\Rightarrow\left\{{}\begin{matrix}2x+1=0\\x-y=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\x=y=-\dfrac{1}{2}\end{matrix}\right.\Rightarrow x=y=-\dfrac{1}{2}\)