TÍNH SABC BIẾT CHU VI TAM GIÁC ABC BẰNG 60cm VÀ AB:BC:CA=3:4:5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
8 tháng 1 2017
(3 cạnh tỉ lệ với 3:4:5 là tam giác vuông đó)
Dễ dàng tính được \(AB=15,BC=20,CA=25\).
Tam giác này vuông tại \(B\).
\(S\left(ABC\right)=\frac{15.10}{2}=65\)
HN
2
CM
29 tháng 9 2018
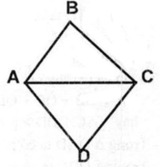
+) Chu vi tứ giác ABCD là: AB + BC + CD + DA = 66 cm (1)
+) Chu vi tam giác ABC là: AB + BC + CA = 56 cm (2)
+) Chu vi tam giác ACD là: AC + CD + AD = 60 cm (3)
Lấy (2) +(3) –(1) vế vế ta được:
(AB +BC + CA) +(AC+CD + AD) – (AB + BC + CD + DA) = 56 + 60 – 66
Hay 2AC = 50 nên AC = 25 cm
13 tháng 7 2015
P kí hiệu là chu vi
Có P(ABCD) = AB + BC + CD + DA = 66
P(ABC) = AB + BC + CA = 56
P(ACD) = AC + CD + DA = 60
=> P (ABC) + P(ACD) = (AB + BC + CD + DA) + 2.AC = 66 + 2.AC = 56 + 60 = 116
=> 2.AC = 116 - 66 = 50 => AC = 50 : 2 = 25
CM
15 tháng 7 2018
Do tam giác ABC đồng dạng với tam giác MNP nên:
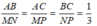
Theo tính chất của dãy tỉ số bằng nhau ta có:
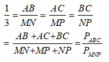
Vậy
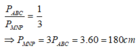
Chọn đáp án A
24 tháng 12 2021
Gọi 3 canh của tam giác lần lượt là x.y.z(cm;x,y,z thuộc N*)
Vì các canh của tam giác tỉ lệ với 3;4;5 và chu vi là 60 nên:
\(\frac{x}{3}\)=\(\frac{y}{4}\)=\(\frac{z}{5}\)và x+y+z=60
Áp dụng tính chất của dãy tỉ số bằng nhau
Ta có:\(\frac{x}{3}\)=\(\frac{y}{4}\)=\(\frac{z}{5}\)=\(\frac{x+y+z}{3+4+5}\)=\(\frac{60}{12}\)=5
Nên:\(\frac{x}{3}\)=5 suy ra x=15
\(\frac{y}{4}\) =5 suy ra y=20
\(\frac{z}{5}\)=5 suy ra z=25
Vậy độ dài 3 cạnh của tam giác lần lượt là 15cm;20cm;25cm.
4 tháng 3 2021
Gọi độ dài ba cạnh của tam giác đó lần lượt là x,y,z.Theo đề bài ta có :
x : y : z = 3 : 4 : 5 hay \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{3+4+5}=\frac{60}{12}=5\)
=> x= 5.3 = 15,y = 5.4 = 20,z = 5.5 = 25
Vậy độ dài của ba cạnh lần lượt là 15cm,20cm,25cm
LM
Lê Minh Vũ
CTVHS
VIP
18 tháng 11 2021
Gọi độ dài 3 cạnh của tam giác lần lượt là \(a,b,c\inℕ^∗;a,b,c\left(cm\right)\)
Do độ dài 3 cạnh tỉ lệ với \(3,4,5\)
\(\Rightarrow\)\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\)
Do chu vi của tam giác là \(60cm\)
\(\Rightarrow\)\(a+b+c=60\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{60}{12}=5\)
Do đó:
\(\frac{a}{3}=5\Rightarrow a=5.3=15\)
\(\frac{b}{4}=5\Rightarrow b=5.4=20\)
\(\frac{c}{5}=5\Rightarrow c=5.5=25\)
Vậy độ dài lần lượt của 3 cạnh tam giác lần lượt là: \(15,20,25\)
KV
2 tháng 12 2023
Ta có:
BC + AC = 60 - 20 = 40 (cm)
Tổng số phần bằng nhau:
3 + 5 = 8 (phần)
BC = 40 : 8 × 3 = 15 (cm)
Câu trả lời của mình đến đây ( bạn tự vẽ hình nha)
Gọi a, b, c lần lượt là các cạnh AB, BC, CA của \(\Delta\) ABC ( a, b, c \(\in\) N )
Theo đề, ta có :
AB:BC:CA = 3:4:5 và AB + BC + CA = 60 ( đề cho)
hay \(\frac{AB}{3}\) = \(\frac{BC}{4}\) = \(\frac{CA}{5}\) và AB + BC + CA = 60
Theo tính chất của dãy tỉ số bằng nhau , ta có :
\(\frac{AB}{3}\) = \(\frac{BC}{4}\) = \(\frac{CA}{5}\) = \(\frac{AB+BC+CA}{3+4+5}\) = \(\frac{60}{3+4+5}\)
= \(\frac{60}{12}\) = 5
\(\frac{AB}{3}\) = 5 => AB = 3.5 = 15 cm
\(\frac{BC}{4}\) = 5 => BC = 4.5 = 20 cm
\(\frac{CA}{5}\) = 5 => CA = 5.5 = 25 cm
\(\Delta\) ABC có:
CA2 = AB2 + BC2
hay 252 = 152 + 202 = 625
=> \(\Delta\) ABC vuông tại B ( dựa vào định lí Py- ta = go )
=> SABC = \(\frac{1}{2}\) AB.AC
= \(\frac{1}{2}\) 15.20
= 150
Vậy diện tích tam giác ABC là 150 cm2
XONG !!!!
ủa tam giác ABC không phải là tam giác cân hạy bạn