Tìm x,y \(\in\) Z sao cho: x*y = 3(x+y)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 12 2023
1, để \(\dfrac{2x+1}{x+3}\) là 1 số nguyên
= > 2x + 1 chia hết cho x + 3 ( x thuộc Z và x \(\ne3\) )
= > 2 ( x + 3 ) - 5 chia hết cho x + 3
=> -5 chia hết cho x + 3
hay x + 3 thuộc Ư(-5 ) \(\in\left\{\pm1;\pm5\right\}\)
Đến đây em tự tìm các giá trị của x
2, Tương tự câu 1, x - 1 chia hết cho x + 5 ( x thuộc Z và x khác - 5 )
= > - 6 chia hết cho x + 5
= > \(x+5\in\left\{\pm1;\pm2;\pm3;\pm6\right\}\)
....
3, ( x - 1 ) ( y - 3 ) = 7
x,y thuộc Z = > x - 1 ; y - 3 thuộc Ư(7)
và ( x - 1 )( y - 3 ) = 7
( 1 ) \(\left\{{}\begin{matrix}x-1=1\\y-3=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=10\end{matrix}\right.\)
(2) \(\left\{{}\begin{matrix}x-1=7\\y-3=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=8\\y=4\end{matrix}\right.\)
( 3) \(\left\{{}\begin{matrix}x-1=-1\\y-3=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-4\end{matrix}\right.\)
( 4 ) \(\left\{{}\begin{matrix}x-1=-7\\y-3=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-6\\y=2\end{matrix}\right.\)
Từ ( 1 ) , ( 2 ) , ( 3 ) , ( 4 ) các cặp giá trị ( x,y ) nguyên cần tìm là ....
PN
24 tháng 9 2016
Ta có : y(x+y+z) + x(x+y+z) + z(x+y+z) = 18 +(-12) + 3
=> (x+y+z)^2 = 9
=> x+y+z = 3 hoặc -3
Xét x+y+z = 3
=> y = 6 ; x = -4 ; z = 1
Xét x+y+z = -3
=> y = -6 ; x= 4 ; z = -1
Vậy (x;y;z) = (6;-4;1) ; (-6;4;-1)
19 tháng 1 2021
a) Ta có: \(\left\{{}\begin{matrix}x+my=2\\mx-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}mx+m^2y=2m\\mx-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2y+2y=2m-1\\mx-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y\left(m^2+2\right)=2m-1\\mx=1+2y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2m-1}{m^2+2}\\x=\dfrac{1+2y}{m}=\left(1+\dfrac{2m-1}{m^2+2}\right)\cdot\dfrac{1}{m}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m^2+2+2m-1}{m^2+2}\cdot\dfrac{1}{m}=\dfrac{m^2+2m+1}{m\left(m^2+2\right)}\\y=\dfrac{2m-1}{m^2+2}\end{matrix}\right.\)
Để hệ phương trình có nghiệm duy nhất thỏa mãn x>0 và y>0 thì \(\left\{{}\begin{matrix}\dfrac{m^2+2m+1}{m\left(m^2+2\right)}>0\\\dfrac{2m-1}{m^2+2}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>0\\2m-1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>0\\m>\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow m>\dfrac{1}{2}>0\)
Vậy: Khi m>0 thì hệ phương trình có nghiệm duy nhất (x,y) thỏa mãn x>0 và y>0
KS
0
HT
2
27 tháng 8 2016
lớp 5 chưa hok cái này nha!!! ^^
5476575676787887987987685876898779346356545645676567
27 tháng 8 2016
Lớp 5 mà học đc thì cux giỏi chẳng kém gì lớp 7 ; 8 !!!!!!!
EC
0
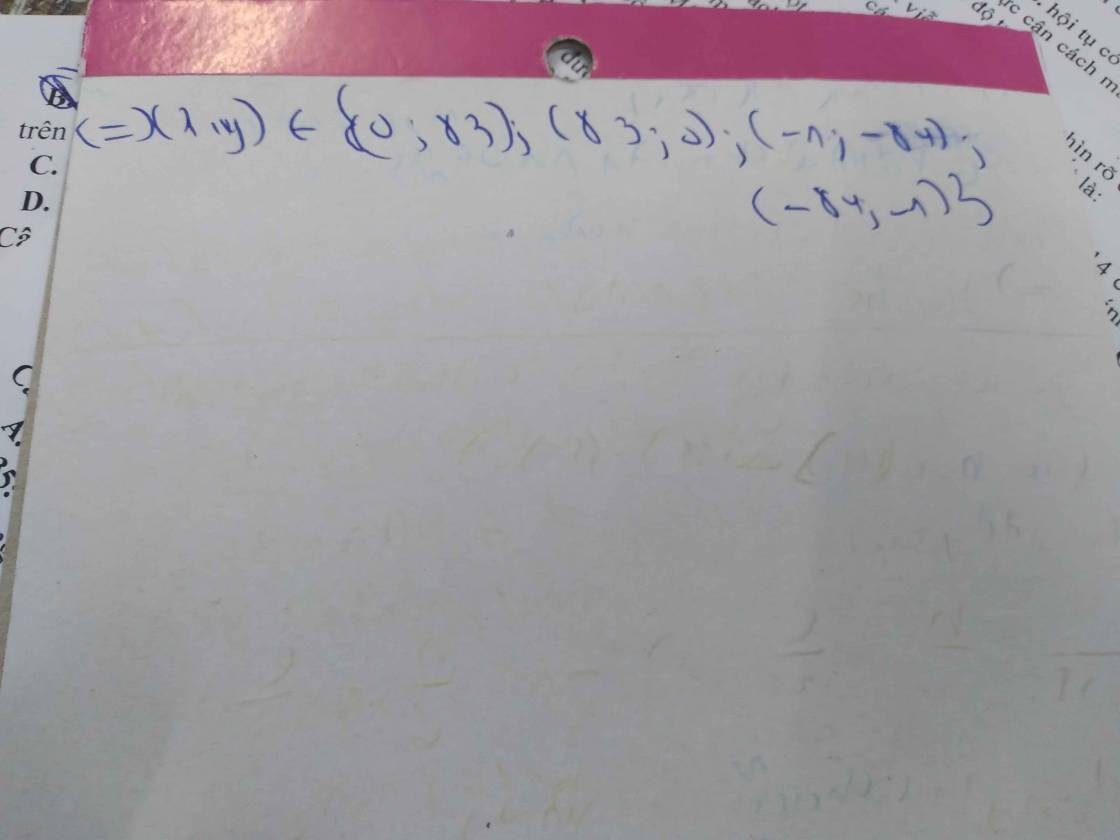
x.y=3.x+3.y
x.y-3.x-3.y=0
x.(y-3)-3.y=0
x.(y-3)-3.y+9=0+9
x.(y-3)-3.(y-3)=9
(x-3).(y-3)=9=3.3=1.9=9.1=(-1).(-9)=(-9).(-1)=(-3).(-3)
Với (x-3).(y-3)=3.3 => x-3=3 => x=6
=> y-3=3=>y=3
Tương tự như trên bạn tự tìm x;y khác nhé