phân tích các đa thức sau thành nhân tử: x2+2x-3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
15 tháng 7 2018
Cách 1: x 2 + 2xy - 15 y 2 = ( x 2 + 2xy + y 2 ) - 16 y 2
= x + y 2 - 4 y 2
= (x + y + 4y)(x + y – 4y)
= (x + 5y)(x – 3y).
Cách 2: x 2 + 2xy - 15 y 2 = x 2 + 5xy – 3xy - 15 y 2
= x(x + 5y) – 3y(x + 5y)
= (x – 3y)(x + 5y).
PT
1
NP
2
2 tháng 8 2021
\(x^2+2x+1-y^2\)
\(=\left(x+1\right)^2-y^2\)
\(=\left(x+1-y\right)\left(x+1+y\right)\)
PT
1
CM
4 tháng 12 2019
x2 + 2x – 3
= x2 + 2x + 1 – 4
= (x + 1)2 – 22
= (x + 1 + 2)(x + 1 – 2)
= (x + 3)(x – 1)
TM
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
27 tháng 12 2023
a/
\(x^2-2x+1=\left(x-1\right)^2\)
b/
\(x^2-5x+xy-5y=x\left(x+y\right)-5\left(x+y\right)=\)
\(=\left(x+y\right)\left(x-5\right)\)
8 tháng 9 2023
a) \(x^2-y^2-3x+3y\)
\(=\left(x-y\right)\left(x+y\right)-3\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y-3\right)\)
b) \(2x+2y-x^2+y^2\)
\(=2\left(x+y\right)-\left(x^2-y^2\right)\)
\(=2\left(x+y\right)-\left(x-y\right)\left(x+y\right)\)
\(=\left(x+y\right)\left(2-x+y\right)\)
c) \(x^2-16+y^2+2xy\)
\(=x^2+y^2+2xy-16\)
\(=\left(x+y\right)^2-16\)
\(=\left(x+y+4\right)\left(x+y-4\right)\)
NX
8 tháng 9 2023
a) \(x^2-y^2-3x+3y\)
\(=\left(ax+y\right)\left(ax-y\right)-3.\left(x-y\right)\)
b) \(2x+2y-x^2+y^2\)
\(=2\left(x+y\right)-\left(x+y\right)\left(x-y\right)\)
c) \(x^2-16+y^2+2xy\)
\(=\left(x+y\right)\left(x-y\right)+2xy-16\)
CM
22 tháng 12 2019
a) Áp dụng HĐT 1 thu được ( 2 x + y ) 2 .
b) Áp dụng HĐT 3 với A = 2x + l; B = x - l thu được
[(2x +1) + (x -1)] [(2x +1) - (x -1)] rút gọn thành 3x(x + 2).
c) Ta có: 9 - 6x + x 2 - y 2 = ( 3 - x ) 2 - y 2 = (3 - x - y)(3 -x + y).
d) Ta có: -(x + 2) + 3( x 2 - 4) = -{x + 2) + 3(x + 2)(x - 2)
= (x + 2) [-1 + 3(x - 2)] = (x + 2)(3x - 7).
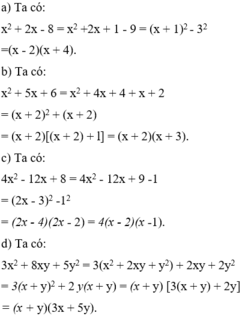
Ta có : x2 + 2x - 3
= x2 - x + 3x - 3
= x(x - 1) + 3(x - 1)
= (x + 3)(x - 1)
x2+2x-3
= ( x + 1 ) ( x - 3 )