Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Em tham khảo bài dưới đây:
Câu hỏi của ngô thị gia linh - Toán lớp 8 - Học toán với OnlineMath
a) \(\Delta AME=\Delta AHE\) (Hai cạnh góc vuông)
a) Do EM = EH và AE vuông góc MH tại E nên AB là đường trung trực của MH. Tương tự AC là trung trực HN.
b) Do AB là đường trung trực của MH nên AM = AH. Tương tự AH = AN
Vậy AM = AN hay tam giác AMN cân tại A.
c) Xét tam giác HMN có E, F lần lượt là trung điểm HM, HN nên EF là đường trung bình tam giác.
Vậy EF // MN.
d) Tam giác cân AMN có I là trung điểm MN nên \(AI⊥MN\)
Lại có MN //EF nên \(AI⊥EF.\)
a) Ta thấy AB vuông góc với MH tại trung điểm E của MH nên AB là đường trung trực của MH.
Ta thấy AC vuông góc với NH tại trung điểm F của NH nên AC là đường trung trực của NH.
b) Do AB là trung trực của MH nên AM = AH.
Tương tự AN = AH. Vậy nên AM = AN hay tam giác AMN cân tại A.
c) Xét tam giác HMN có E là trung điểm MH, F là trung điểm HN nên EF là đường trung bình tam giác HMN.
Suy ra EF // MN.
d) Do tam giác AMN cân tại A nên trung tuyến AI đồng thời là đường cao. Vậy AI vuông góc MN.
Lại có MN // EF nên AI vuông góc EF.
xét 2 tam giác MBE và tam giác HBE =
=> MB=HB
xét 2 tam giác AME = tam giác AHE
=> AM=HA
xét 2 tam giác BMA và tam giác BHA có
BA chung
BM=BH
MA=MH
=> 2 tam giác =
mà góc BHA vuông góc
=> BMA vuông góc
=> BM vuông góc với AM
câu b thì mình vẽ nó song song cơ... gửi cho mình cái hình nha
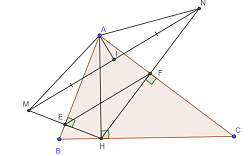
a/ Ta có : AE là cạnh chung của hai tam giác vuông: tam giác AME và tam giác AHE ; ME = EM (gt)
=> tam giác AME = tam giác AHE (2 cạnh góc vuông)
b/ Dễ thấy EH = EM ; AB vuông góc MH => đpcm
Tương tự với AC .
c/ Ta chứng minh được : AB là đường trung trực của MH
=> AM = AH (1)
AC là đường trung trực của NH => AH = AN (2)
Từ (1) và (2) suy ra AM = AN => tam giác AMN cân tại A
d/ Hãy chứng minh MN // EF