Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta thấy AB vuông góc với MH tại trung điểm E của MH nên AB là đường trung trực của MH.
Ta thấy AC vuông góc với NH tại trung điểm F của NH nên AC là đường trung trực của NH.
b) Do AB là trung trực của MH nên AM = AH.
Tương tự AN = AH. Vậy nên AM = AN hay tam giác AMN cân tại A.
c) Xét tam giác HMN có E là trung điểm MH, F là trung điểm HN nên EF là đường trung bình tam giác HMN.
Suy ra EF // MN.
d) Do tam giác AMN cân tại A nên trung tuyến AI đồng thời là đường cao. Vậy AI vuông góc MN.
Lại có MN // EF nên AI vuông góc EF.

A B C H E M F N
a/ Ta có : AE là cạnh chung của hai tam giác vuông: tam giác AME và tam giác AHE ; ME = EM (gt)
=> tam giác AME = tam giác AHE (2 cạnh góc vuông)
b/ Dễ thấy EH = EM ; AB vuông góc MH => đpcm
Tương tự với AC .
c/ Ta chứng minh được : AB là đường trung trực của MH
=> AM = AH (1)
AC là đường trung trực của NH => AH = AN (2)
Từ (1) và (2) suy ra AM = AN => tam giác AMN cân tại A
d/ Hãy chứng minh MN // EF

Em tham khảo bài dưới đây:
Câu hỏi của ngô thị gia linh - Toán lớp 8 - Học toán với OnlineMath
a) \(\Delta AME=\Delta AHE\) (Hai cạnh góc vuông)

xét 2 tam giác MBE và tam giác HBE =
=> MB=HB
xét 2 tam giác AME = tam giác AHE
=> AM=HA
xét 2 tam giác BMA và tam giác BHA có
BA chung
BM=BH
MA=MH
=> 2 tam giác =
mà góc BHA vuông góc
=> BMA vuông góc
=> BM vuông góc với AM
câu b thì mình vẽ nó song song cơ... gửi cho mình cái hình nha

a) Ta có: EH = EM (gt); AB ⊥ HE (gt).
⇒ AB là đường trực của MH. (đpcm1)
CMTT, ta được: AC là đường trực của NH. (đpcm2)
b) Ta có: AB là đường trực của MH. (cmt)
⇒ AM = AH. (1)
CMTT, ta được: AN = AH. (2)
Từ (1), (2) ⇒ AM = AN.
△AMN có: AM = AN. (cmt)
⇒ △AMN cân tại A. (đpcm)
c) △HMN có: EH = EM (gt); FH = FN (gt).
⇒ EF là đường trung bình của △HMN.
⇒ EF // MN. (đpcm)
d) △AMN cân ở A. (cmt)
⇒ Đường trung truyến AI (IM = IN) cũng là đường cao.
⇒ AI ⊥ MN.
Mà EF // MN. ⇒ AI ⊥EF. (đpcm)

a: Ta có: AB vuông góc với HM tại E
mà E la trung điểm của HM
nên AB là trung trực của MH
Ta có: AC vuông góc với HN tại F
mà F la trung điểm của HN
nên AC là đừog trug trực của HN
b: Ta có: AM=AH
AN=AH
DO đó; AM=AN
hay ΔAMN can tại A
c: Xét ΔHNM có HE/EM=HF/FN
nên FE//MN
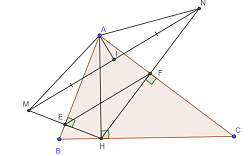


Đoạn thẳng f: Đoạn thẳng [A, B] Đoạn thẳng g: Đoạn thẳng [B, C] Đoạn thẳng h: Đoạn thẳng [A, C] Đoạn thẳng j: Đoạn thẳng [A, H] Đoạn thẳng k: Đoạn thẳng [H, M] Đoạn thẳng l: Đoạn thẳng [N, H] Đoạn thẳng m: Đoạn thẳng [M, N] Đoạn thẳng n: Đoạn thẳng [A, N] Đoạn thẳng p: Đoạn thẳng [A, M] Đoạn thẳng q: Đoạn thẳng [E, F] Đoạn thẳng r: Đoạn thẳng [A, I] Đoạn thẳng t: Đoạn thẳng [I, D] A = (9.91, 10.29) A = (9.91, 10.29) A = (9.91, 10.29) B = (3.97, -8.27) B = (3.97, -8.27) B = (3.97, -8.27) C = (33.4, -8.47) C = (33.4, -8.47) C = (33.4, -8.47) Điểm H: Giao điểm đường của i, g Điểm H: Giao điểm đường của i, g Điểm H: Giao điểm đường của i, g Điểm M: H đối xứng qua f Điểm M: H đối xứng qua f Điểm M: H đối xứng qua f Điểm N: H đối xứng qua h Điểm N: H đối xứng qua h Điểm N: H đối xứng qua h Điểm E: Giao điểm đường của f, k Điểm E: Giao điểm đường của f, k Điểm E: Giao điểm đường của f, k Điểm F: Giao điểm đường của h, l Điểm F: Giao điểm đường của h, l Điểm F: Giao điểm đường của h, l Điểm I: Trung điểm của m Điểm I: Trung điểm của m Điểm I: Trung điểm của m Điểm D: Giao điểm đường của s, q Điểm D: Giao điểm đường của s, q
a) Do EM = EH và AE vuông góc MH tại E nên AB là đường trung trực của MH. Tương tự AC là trung trực HN.
b) Do AB là đường trung trực của MH nên AM = AH. Tương tự AH = AN
Vậy AM = AN hay tam giác AMN cân tại A.
c) Xét tam giác HMN có E, F lần lượt là trung điểm HM, HN nên EF là đường trung bình tam giác.
Vậy EF // MN.
d) Tam giác cân AMN có I là trung điểm MN nên \(AI⊥MN\)
Lại có MN //EF nên \(AI⊥EF.\)