Toán thi vào lớp 10 đây
Bài 1:
Giải các phương trình và hệ phương trình sau:
a) x2 - 8x + 15 = 0.
b) 2x2 - √2x - 2 = 0.
c) x4 - 5x2 - 6 = 0.
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,x^2-6x+5=0\\ \Rightarrow\left(x^2-5x\right)-\left(x-5\right)=0\\ \Rightarrow x\left(x-5\right)-\left(x-5\right)=0\\ \Rightarrow\left(x-1\right)\left(x-5\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
\(b,2x^2+4x-8=0\\ \Rightarrow x^2+2x-4=0\\ \Rightarrow\left(x^2+2x+1\right)-5=0\\ \Rightarrow\left(x+1\right)^2-\sqrt{5^2}=0\\ \Rightarrow\left(x+1+\sqrt{5}\right)\left(x+1-\sqrt{5}\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=-1-\sqrt{5}\\x=-1+\sqrt{5}\end{matrix}\right.\)
\(c,4y^2-4y+1=0\\ \Rightarrow\left(2y-1\right)^2=0\\ \Rightarrow2y-1=0\\ \Rightarrow y=\dfrac{1}{2}\)
\(d,5x^2-x+2=0\)
Ta có:\(\Delta=\left(-1\right)^2-4.5.2=1-40=-39\)
Vì \(\Delta< 0\Rightarrow\) pt vô nghiệm

2:
\(A=\dfrac{x_2-1+x_1-1}{x_1x_2-\left(x_1+x_2\right)+1}\)
\(=\dfrac{3-2}{-7-3+1}=\dfrac{1}{-9}=\dfrac{-1}{9}\)
B=(x1+x2)^2-2x1x2
=3^2-2*(-7)
=9+14=23
C=căn (x1+x2)^2-4x1x2
=căn 3^2-4*(-7)=căn 9+28=căn 27
D=(x1^2+x2^2)^2-2(x1x2)^2
=23^2-2*(-7)^2
=23^2-2*49=431
D=9x1x2+3(x1^2+x2^2)+x1x2
=10x1x2+3*23
=69+10*(-7)=-1

a) Ta có:Δ =(-7)2 -4.2.2 =49 -16 =33 >0
Phương trình có 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 =-b/a =7/2 ;x1x2 =c/a =2/2 =1
b) c = -16 suy ra ac < 0
Phương trình có 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 =-b/a =-2/5 ;x1x2 =c/a =-16/5
c) Ta có: Δ’ = 22 – (2 -√3 )(2 + √2 ) =4 -4 - 2√2 +2√3 +√6
= 2√3 - 2√2 +√6 >0
Phương trình 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
d) Ta có : Δ = (-3)2 -4.1,4.1,2 =9 – 6,72 =2,28 >0
Phương trình có 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 = -b/a = 3/(1.4) = 30/14 = 15/7 ; x1x2 = c/a = (1.2)/(1.4) = 12/14 = 6/7
Ta có: Δ = 12 -4.5.2 = 1 - 40 = -39 < 0

+ 2x2 + y2 – 8x + 2y – 1 = 0 không phải phương trình đường tròn vì hệ số của x2 khác hệ số của y2.
+ Phương trình x2 + y2 + 2x – 4y – 4 = 0 có :
a = –1; b = 2; c = –4 ⇒ a2 + b2 – c = 9 > 0
⇒ phương trình trên là phương trình đường tròn.
+ Phương trình x2 + y2 – 2x – 6y + 20 = 0 có :
a = 1; b = 3; c = 20 ⇒ a2 + b2 – c = –10 < 0
⇒ phương trình trên không là phương trình đường tròn.
+ Phương trình x2 + y2 + 6x + 2y + 10 = 0 có :
a = –3; b = –1; c = 10 ⇒ a2 + b2 – c = 0 = 0
⇒ phương trình trên không là phương trình đường tròn.

câu 1
a) 5x(x-2)=0 =>\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
b)(x+5)(2x-7)=0 =>\(\left[{}\begin{matrix}x+5=0\\2x-7=0\end{matrix}\right.\)=>\(\left[{}\begin{matrix}x=-5\\x=\dfrac{7}{2}\end{matrix}\right.\)
c) \(\dfrac{5x}{x+2}\)=4 Đk x\(\ne\)-2
=> 5x=4(x+2)
=>5x-4x=8
=>x=8(tmđk)

a) 2 x 2 – 17 x + 1 = 0
Có a = 2; b = -17; c = 1
Δ = b 2 – 4 a c = ( - 17 ) 2 – 4 . 2 . 1 = 281 > 0 .
Theo hệ thức Vi-et: phương trình có hai nghiệm x1; x2 thỏa mãn:
x 1 + x 2 = − b / a = 17 / 2 x 1 x 2 = c / a = 1 / 2
b) 5 x 2 – x – 35 = 0
Có a = 5 ; b = -1 ; c = -35 ;
Δ = b 2 – 4 a c = ( - 1 ) 2 – 4 . 5 . ( - 35 ) = 701 > 0
Theo hệ thức Vi-et, phương trình có hai nghiệm x1; x2 thỏa mãn:
x 1 + x 2 = − b / a = 1 / 5 x 1 ⋅ x 2 = c / a = − 35 / 5 = − 7
c) 8 x 2 – x + 1 = 0
Có a = 8 ; b = -1 ; c = 1
Δ = b 2 – 4 a c = ( - 1 ) 2 – 4 . 8 . 1 = - 31 < 0
Phương trình vô nghiệm nên không tồn tại x1 ; x2.
d) 25 x 2 + 10 x + 1 = 0
Có a = 25 ; b = 10 ; c = 1
Δ = b 2 – 4 a c = 10 2 – 4 . 25 . 1 = 0
Khi đó theo hệ thức Vi-et có:
x 1 + x 2 = − b / a = − 10 / 25 = − 2 / 5 x 1 x 2 = c / a = 1 / 25

Cả ba phương trình trên đều là phương trình trùng phương.
a) 3 x 4 – 12 x 2 + 9 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 3 t 2 – 12 t + 9 = 0 ( 2 )
Giải (2):
Có a = 3; b = -12; c = 9
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t 1 = 1 v à t 2 = 3 .
Cả hai nghiệm đều thỏa mãn điều kiện.
+ t = 3 ⇒ x 2 = 3 ⇒ x = ± 3 + t = 1 ⇒ x 2 = 1 ⇒ x = ± 1
Vậy phương trình có tập nghiệm 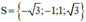
b) 2 x 4 + 3 x 2 – 2 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 2 t 2 + 3 t – 2 = 0 ( 2 )
Giải (2) :
Có a = 2 ; b = 3 ; c = -2
⇒ Δ = 3 2 – 4 . 2 . ( - 2 ) = 25 > 0
⇒ (2) có hai nghiệm
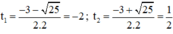
t 1 = - 2 < 0 nên loại.
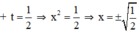
Vậy phương trình có tập nghiệm 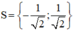
c) x 4 + 5 x 2 + 1 = 0 ( 1 )
Đặt x 2 = t , t > 0 .
(1) trở thành: t 2 + 5 t + 1 = 0 ( 2 )
Giải (2):
Có a = 1; b = 5; c = 1
⇒ Δ = 5 2 – 4 . 1 . 1 = 21 > 0
⇒ Phương trình có hai nghiệm:
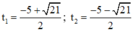
Cả hai nghiệm đều < 0 nên không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
Giải các phương trình và hệ phương trình sau:
a) x2 - 8x + 15 = 0.
Δ' = 42 - 15 = 1
↔ x = 4 + 1 = 5 hay x = 4 - 1 = 3
b) 2x2 - √2x - 2 = 0. (2)
Δ = 2 - 4(2)(-2) = 18
(2) ↔ x = (√2 + 3√2)/4 = √2 hay x = (√2 - 3√2)/4 = -√2/2
c) x4 - 5x2 - 6 = 0
Đặt u = x2 ≥ 0 pt thành:
u2 - 5u - 6 = 0 ↔ u = -1 (loại) hay u = 6
Do đó pt ↔ x2 = 6 ↔ x = ±√6.