Tìm m để y = \(\frac{x^2+mx+1}{x+m}\) đạt cực đại tại x = 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 5 2021
a.
\(y'=x^2+2\left(m^2-1\right)x+2m-3\)
\(y''=2x+2\left(m^2-1\right)\)
Hàm đạt cực đại tại \(x=2\) khi: \(\left\{{}\begin{matrix}y'\left(2\right)=0\\y''\left(2\right)< 0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}4+4\left(m^2-1\right)+2m-3=0\\4+2\left(m^2-1\right)< 0\end{matrix}\right.\)
Do \(2m^2+2>0\) ;\(\forall m\) nên ko tồn tại m thỏa mãn yêu cầu đề bài
b.
\(y'=x^2+2mx+3\)
\(y''=2x+2m\)
Hàm đạt cực đại tại \(x=-3\) khi: \(\left\{{}\begin{matrix}9-6m+3=0\\-6+2m< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m=2\\m< 3\end{matrix}\right.\)
\(\Rightarrow m=2\)
CM
19 tháng 12 2018
a) y′ = 3 x 2 + 2(m + 3)x + m
y′ = 0 ⇔ 3 x 2 + 2(m + 3)x + m = 0
Hàm số đạt cực trị tại x = 1 thì:
y′(1) = 3 + 2(m + 3) + m = 3m + 9 = 0 ⇔ m = −3
Khi đó,
y′ = 3 x 2 – 3;
y′′ = 6x;
y′′(1) = 6 > 0;
Suy ra hàm số đạt cực tiểu tại x = 1 khi m = 3.
b) y′ = −( m 2 + 6m) x 2 − 4mx + 3
y′(−1) = − m 2 − 6m + 4m + 3 = (− m 2 − 2m – 1) + 4 = −(m + 1)2 + 4
Hàm số đạt cực trị tại x = -1 thì :
y′(−1) = − ( m + 1 ) 2 + 4 = 0 ⇔ ( m + 1 ) 2 = 4
⇔ 
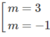
Với m = -3 ta có y’ = 9 x 2 + 12x + 3
⇒ y′′ = 18x + 12
⇒ y′′(−1) = −18 + 12 = −6 < 0
Suy ra hàm số đạt cực đại tại x = -1.
Với m = 1 ta có:
y′ = −7 x 2 − 4x + 3
⇒ y′′ = −14x − 4
⇒ y′′(−1) = 10 > 0
Suy ra hàm số đạt cực tiểu tại x = -1
Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.
VH
1
23 tháng 4 2016
Tập xác định : \(D=R\backslash\left\{-m\right\}\)
Ta có : \(y=x+\frac{1}{x+m}\Rightarrow y'=1-\frac{1}{\left(x+m\right)^2}\Rightarrow y"=\frac{2}{\left(x+m\right)^3}\)
Hàm số đạt cực tiểu tại \(x=1\Leftrightarrow\begin{cases}y'\left(1\right)=0\\y"\left(1\right)>0\end{cases}\)
\(\Leftrightarrow\begin{cases}1-\frac{1}{\left(x+m\right)^2}=0\\\frac{2}{\left(x+m\right)^3}>0\end{cases}\) \(\Leftrightarrow\begin{cases}m^2+2m=0\\m>-1\end{cases}\) \(\Leftrightarrow m=0\)
Vậy m = 0 thì hàm số đạt cực tiểu tạo x = 1
LM
1
11 tháng 7 2016
TXD D=R
y'=3x^2-2mx+m-2/3.
nếu hs đạt cực tiểu tại x=1 thì y'(1)=0
<=>3-2m+m-2/3=0<=>m=7/3
khi m=7/3 thì y'=3x^2-14/3x+5/3=0 y''=6x-14/3
ta có y'=0<=>x=1 hoặc x=5/9 =>y''(1)=6-14/3=4/3 >0
vậy tại m=7/3 là điểm cực tiểu tại x=1
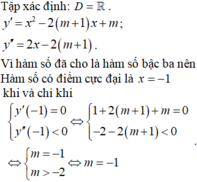
TXD X khác -m
y'=x^2 +2mx+m^2-1
nếu hs đạt CĐ tại x=2 thì y'(2)=0
<=>m^2 +4m+3=0 nên m=-1 hoặc -3
khi m=-1 thi y'=x^2+2x nên y'=0 thì x=o hoặc x=2
y''=2x+2=>y''(2)=6>0 =>m=-1 khon phải điểm cực đại
khi m=-3
khi m=-1 thi y'=x^2-6x+8 nên y'=0 thì x=4 hoặc x=2
y''=2x-6=>y''(2)=-2>0 =>m=-3 điểm cực đại tại x=2
tim txd => tinh y' =>y'' => thay 2 vao y' va y''<=>y'(2)=o va y''(2)<0 => tim dc m