Cho hình lăng trụ ABC.A'B'C'. Gọi M. N theo thứ tự là trung điểm các cạnh BB', C'A' và P là điểm trên cạnh B'C' sao cho C'P = 2PB'.
Chứng minh rằng A, M, N và P đồng phẳng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Ta có: S B M C N = B M + C N 2 d B B ' ; C C ' = B B ' 2 + 3 4 C C ' 2 d B B ' ; C C ' = 5 8 B B ' . d B B ' ; C C '
Do đó V 2 = 5 8 V A . B C C ' B ' = 5 8 . 2 3 V (với V = V A B C . A ' B ' C ' ) = 5 12 V
Suy ra V 1 = 7 12 V ⇒ V 1 V 2 = 7 5 .

Chọn D
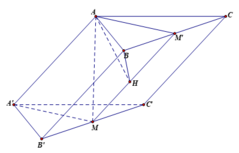
Kéo dài MH cắt BC tại M'. Ta có
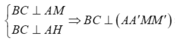
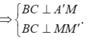
Tại có:
![]()
![]()
nên tam giác AMM' vuông tại A
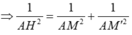
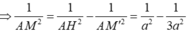
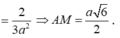
Do
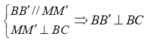
nên tứ giác BB'C'C là hình chữ nhật.
Do đó:
![]()
![]()
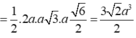
Đặt \(\overrightarrow{AB}=\overrightarrow{a}\) , \(\overrightarrow{AC}=\overrightarrow{b}\) và \(\overrightarrow{AA'}=\overrightarrow{c}\) khi đó
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{a}+\frac{1}{2}.\overrightarrow{c}\)
\(\overrightarrow{AN}=\overrightarrow{AA'}+\overrightarrow{A'N}=\frac{1}{2}.\overrightarrow{b}+\overrightarrow{c}\)
\(\overrightarrow{AP}=\overrightarrow{AB}'+\overrightarrow{B'P}=\frac{2}{3}\overrightarrow{a}+\frac{1}{3}.\overrightarrow{b}+\overrightarrow{c}\)
Do \(c\frac{2}{3}.\overrightarrow{a}+\frac{1}{3}.\overrightarrow{b}+\overrightarrow{c}=\frac{2}{3}\left(\overrightarrow{a}+\frac{1}{2}.\overrightarrow{c}\right)+\frac{2}{3}\left(\frac{1}{2}.\overrightarrow{b}+\overrightarrow{c}\right)\)
Nên \(3\overrightarrow{AP}=2\overrightarrow{AM}+2\overrightarrow{AN}\)
Suy ra A, M, N, P đồng phẳng