giải pt
√4x2−4x+1+2=3x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, \(x^4-4x^3-6x^2-4x+1=0\)(*)
<=> \(x^4+4x^2+1-4x^3-4x+2x^2-12x^2=0\)
<=> \(\left(x^2-2x+1\right)^2=12x^2\)
<=>\(\left(x-1\right)^4=12x^2\) <=> \(\left[{}\begin{matrix}\left(x-1\right)^2=\sqrt{12}x\\\left(x-1\right)^2=-\sqrt{12}x\end{matrix}\right.\)<=> \(\left[{}\begin{matrix}x^2-2x+1-\sqrt{12}x=0\left(1\right)\\x^2-2x+1+\sqrt{12}x=0\left(2\right)\end{matrix}\right.\)
Giải (1) có: \(x^2-2x+1-\sqrt{12}x=0\)
<=> \(x^2-2x\left(1+\sqrt{3}\right)+\left(1+\sqrt{3}\right)^2-\left(1+\sqrt{3}\right)^2+1=0\)
<=> \(\left(x-1-\sqrt{3}\right)^2-3-2\sqrt{3}=0\)
<=> \(\left(x-1-\sqrt{3}\right)^2=3+2\sqrt{3}\) <=> \(\left[{}\begin{matrix}x-1-\sqrt{3}=\sqrt{3+2\sqrt{3}}\\x-1-\sqrt{3}=-\sqrt{3+2\sqrt{3}}\end{matrix}\right.\) <=> \(\left[{}\begin{matrix}x=\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\left(ktm\right)\\x=-\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\left(tm\right)\end{matrix}\right.\)
=> \(x=-\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\)
Giải (2) có: \(x^2-2x+1+\sqrt{12}x=0\)
<=> \(x^2-2x\left(1-\sqrt{3}\right)+\left(1-\sqrt{3}\right)^2-\left(1-\sqrt{3}\right)^2+1=0\)
<=> \(\left(x+\sqrt{3}-1\right)^2=3-2\sqrt{3}\) .Có VP<0 => PT (2) vô nghiệm
Vậy pt (*) có nghiệm x=\(-\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\)

a: =>17x-5x-15-2x-5=0
=>10x-20=0
=>x=2
b: =>\(\dfrac{3x-6-5x-10}{\left(x+2\right)\left(x-2\right)}=\dfrac{11x+23}{\left(x+2\right)\left(x-2\right)}\)
=>11x+23=-2x-16
=>13x=-39
=>x=-3(nhận)
c: =>5x+7>=3x-3
=>2x>=-10
=>x>=-5
d: =>5(3x-1)=-2(x+1)
=>15x-5=-2x-2
=>17x=3
=>x=3/17
e: =>4x^2-1-4x^2-3x-2=0
=>-3x-3=0
=>x=-1
g: =>7x-5-8x+2-7<0
=>-x-10<0
=>x+10>0
=>x>-10

a: =>17x-5x-15-2x-5=0
=>10x-20=0
=>x=2
b: =>\(\dfrac{3x-6-5x-10}{\left(x+2\right)\left(x-2\right)}=\dfrac{11x+23}{\left(x+2\right)\left(x-2\right)}\)
=>11x+23=-2x-16
=>13x=-39
=>x=-3(nhận)
c: =>5x+7>=3x-3
=>2x>=-10
=>x>=-5
d: =>5(3x-1)=-2(x+1)
=>15x-5=-2x-2
=>17x=3
=>x=3/17
e: =>4x^2-1-4x^2-3x-2=0
=>-3x-3=0
=>x=-1
g: =>7x-5-8x+2-7<0
=>-x-10<0
=>x+10>0
=>x>-10

a) \(2x^2-5x+1=0\)
\(\Delta=b^2-4ac\Rightarrow\left(-5\right)^2-4.2.1=17>0\)
Phương trình có 2 nghiệm phân biệt:
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-\left(-5\right)+\sqrt{17}}{2.2}=\dfrac{5+\sqrt{17}}{4}\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-\left(-5\right)-\sqrt{17}}{2.2}=\dfrac{5-\sqrt{17}}{4}\)
___________________________________________________
b) \(4x^2+4x+1=0\)
\(\Delta=b^2-4ac\Rightarrow4^2-4.4.1=0\)
Vậy phương trình có nghiệm kép:
___________________________________________________
c) \(5x^2-x+2=0\)
\(\Delta=b^2-4a\Rightarrow\left(-1\right)^2-4.5.2=-39\)
Vậy phương trình vô nghiệm.

Ta có : x4+3x3+4x2+3x+1=0
⇔ ( x4 + x3 ) + ( 2x3 + 2x2 ) + ( 2x2 + 2x ) + ( x + 1 ) = 0
⇔ x3 ( x + 1 ) + 2x2 ( x + 1 ) + 2x ( x+1 ) + ( x + 1 ) =0
⇔ ( x + 1 ) ( x3 + 2x2 + 2x + 1 ) = 0
⇔ ( x + 1 ) [ ( x3 + 1 ) + ( 2x2 + 2x ) ] = 0
⇔ ( x + 1 ) [ (x + 1 ) ( x2 - x +1 ) + 2x ( x + 1 ) ] =0
⇔ ( x +1 ) ( x + 1 ) ( x2 + x +1 ) =0
⇒ \(\left[{}\begin{matrix}x+1=0\\x^{2^{ }}+x+1=0\end{matrix}\right.\)<=> \(\left[{}\begin{matrix}x=-1\\\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}=0\left(VoLy\right)\end{matrix}\right.\)
Vậy x = -1
x4+3x3+4x2+3x+1=0
⇔(x4+2x3+x2)+(x3+2x2+1)+(x2+2x+1)=0
⇔x2(x2+2x+1)+x(x2+2x+1)+(x2+2x+1)=0
⇔x2(x+1)2+x(x+1)2+(x+1)2=0
⇔(x+1)2(x2+x+1)=0
Vì x2+x+1=x2+x+\(\dfrac{1}{4}\)+\(\dfrac{3}{4}\)=(x+\(\dfrac{1}{2}\))2+\(\dfrac{3}{4}\)>0 nên phương trình đã cho tương đương:
(x+1)2=0 ⇔(x+1)(x+1)=0 ⇔x=-1.


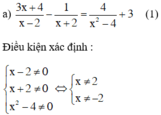
Quy đồng và bỏ mẫu chung ta được:
Phương trình (1) ⇔ (3x + 4)(x + 2) – (x – 2) = 4 + 3(x2 – 4)
⇔ 3x2 + 6x + 4x + 8 – x + 2 = 4 + 3x2 – 12
⇔ 9x = –18
⇔ x = –2 (không thỏa mãn đkxđ)
Vậy phương trình vô nghiệm.

a: =>(2x-5x-1)(2x+5x+1)=0
=>(-3x-1)(7x+1)=0
=>x=-1/3 hoặc x=-1/7
b: =>(5x-5)^2-(x+2)^2=0
=>(5x-5-x-2)(5x-5+x+2)=0
=>(4x-7)(6x-3)=0
=>x=1/2 hoặc x=7/4
c: =>(x^2+4x-1-x^2+3x-2)(x^2+4x-1+x^2-3x+2)=0
=>(7x-3)(2x^2+x+1)=0
=>7x-3=0
=>x=3/7
\(\sqrt{4x^2-4x+1}=3x-2\)
\(\sqrt{\left(2x-1\right)^2}=3x-2\)
\(\left|2x-1\right|=3x-2\)
\(\orbr{\begin{cases}2x-1=3x-2\\2x-1=-3x+2\end{cases}}\)
\(\orbr{\begin{cases}1=x\\5x=1\end{cases}}\)
\(\orbr{\begin{cases}x=1\\x=\frac{1}{5}\end{cases}}\)
ĐKXĐ: \(x\ge\frac{2}{3}\)
Ta có : \(\sqrt{4x^2-2x+1}+2=3x\)
\(\Leftrightarrow\sqrt{\left(2x-1\right)^2}=3x-2\)
\(\Leftrightarrow|2x-1|=3x-2\)
\(\Leftrightarrow2x-1=3x-2\)(do \(x\ge\frac{2}{3}\))
\(\Leftrightarrow x=1\left(TM\right)\)
Vậy tập nghiệm của PT là \(S=\left\{1\right\}\)