K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NS
3
Những câu hỏi liên quan
15 tháng 6 2023
B/A
\(=\dfrac{1+\dfrac{2020}{2}+1+\dfrac{2019}{3}+...+1+\dfrac{1}{2021}+1}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}+\dfrac{1}{2022}}\)
\(=\dfrac{2022\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}+\dfrac{1}{2022}\right)}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}+\dfrac{1}{2022}}=2022\)
BL
0
BL
1
4 tháng 10 2020
a) Ta có: \(\sqrt{2021}-\sqrt{2020}\)
\(=\frac{\left(\sqrt{2021}-\sqrt{2020}\right)\left(\sqrt{2021}+\sqrt{2020}\right)}{\sqrt{2021}+\sqrt{2020}}\)
\(=\frac{1}{\sqrt{2020}+\sqrt{2021}}\)
Ta có: \(\sqrt{2020}-\sqrt{2019}\)
\(=\frac{\left(\sqrt{2020}-\sqrt{2019}\right)\left(\sqrt{2020}+\sqrt{2019}\right)}{\sqrt{2020}+\sqrt{2019}}\)
\(=\frac{1}{\sqrt{2019}+\sqrt{2020}}\)
Ta có: \(\sqrt{2020}+\sqrt{2021}>\sqrt{2019}+\sqrt{2020}\)
\(\Leftrightarrow\frac{1}{\sqrt{2020}+\sqrt{2021}}< \frac{1}{\sqrt{2019}+\sqrt{2020}}\)
hay \(\sqrt{2021}-\sqrt{2020}< \sqrt{2020}-\sqrt{2019}\)
b) Ta có: \(\sqrt{2019\cdot2021}\)
\(=\sqrt{\left(2020-1\right)\left(2020+1\right)}\)
\(=\sqrt{2020^2-1}\)
Ta có: \(2020=\sqrt{2020^2}\)
Ta có: \(2020^2-1< 2020^2\)
nên \(\sqrt{2020^2-1}< \sqrt{2020^2}\)
\(\Leftrightarrow\sqrt{2019\cdot2021}< 2020\)
c) Ta có: \(\left(\sqrt{2019}+\sqrt{2021}\right)^2\)
\(=2019+2021+2\cdot\sqrt{2019\cdot2021}\)
\(=4040+2\sqrt{2019\cdot2021}\)
\(=4040+2\cdot\sqrt{2020^2-1}\)
Ta có: \(\left(2\sqrt{2020}\right)^2\)
\(=4\cdot2020\)
\(=4040+2\cdot2020\)
\(=4040+2\cdot\sqrt{2020^2}\)
Ta có: \(2020^2-1< 2020^2\)
\(\Leftrightarrow\sqrt{2020^2-1}< \sqrt{2020^2}\)
\(\Leftrightarrow2\cdot\sqrt{2020^2-1}< 2\cdot\sqrt{2020^2}\)
\(\Leftrightarrow4040+2\cdot\sqrt{2020^2-1}< 4040+2\cdot\sqrt{2020^2}\)
\(\Leftrightarrow\left(\sqrt{2019}+\sqrt{2021}\right)^2< \left(2\sqrt{2020}\right)^2\)
\(\Leftrightarrow\sqrt{2019}+\sqrt{2021}< 2\sqrt{2020}\)
BD
16 tháng 7 2023
a) Ta có:
2A=2.(12+122+123+...+122020+122021)2�=2.12+122+123+...+122 020+122 021
2A=1+12+122+123+...+122019+1220202�=1+12+122+123+...+122 019+122 020
Suy ra: 2A−A=(1+12+122+123+...+122019+122020)2�−�=1+12+122+123+...+122 019+122 020
−(12+122+123+...+122020+122021)−12+122+123+...+122 020+122 021
Do đó A=1−122021<1�=1−122021<1.
Lại có B=13+14+15+1360=20+15+12+1360=6060=1�=13+14+15+1360=20+15+12+1360=6060=1.
Vậy A < B.
9 tháng 8 2019
bài 1:
ssh của A là:
(151-3):2+1=75
A=(151+3)x75:2=5775
đáp số: 5775
12 tháng 12 2021
S = \(\left(1+\dfrac{1}{3}+...+\dfrac{1}{2021}\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2020}\right)\)
= \(\left(1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2021}\right)-2.\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2020}\right)\)
= \(\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}\right)-\left(1+\dfrac{1}{2}+...+\dfrac{1}{1010}\right)\)
= \(\dfrac{1}{1011}+\dfrac{1}{1012}+...+\dfrac{1}{2021}\)
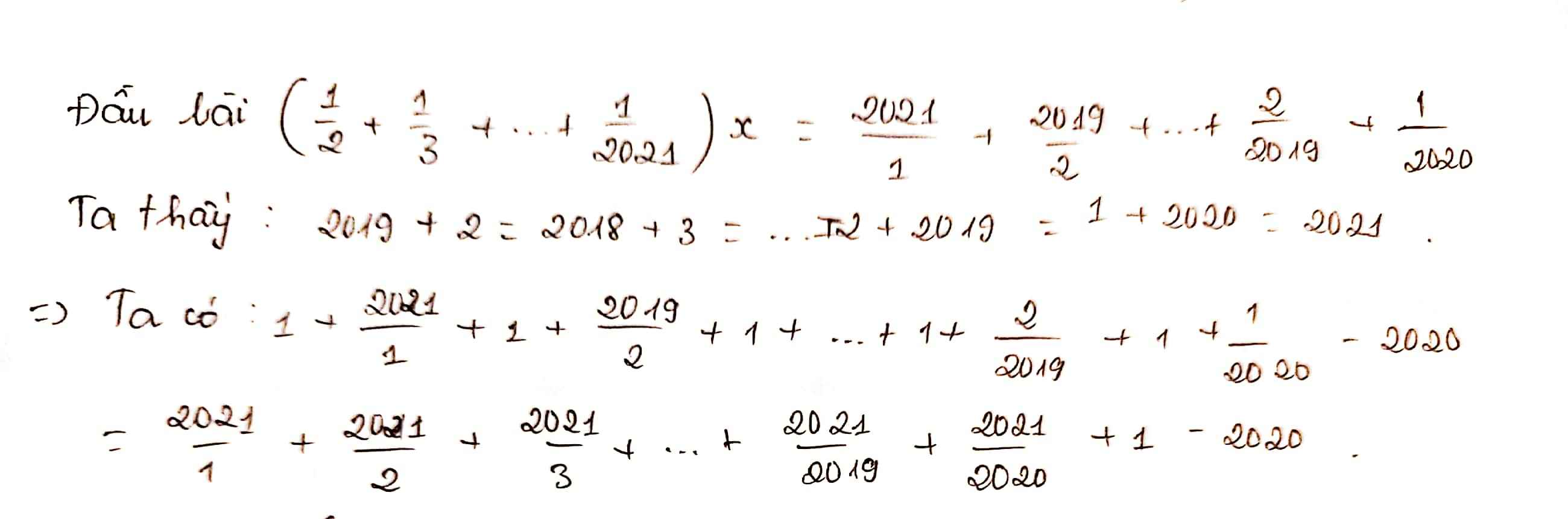
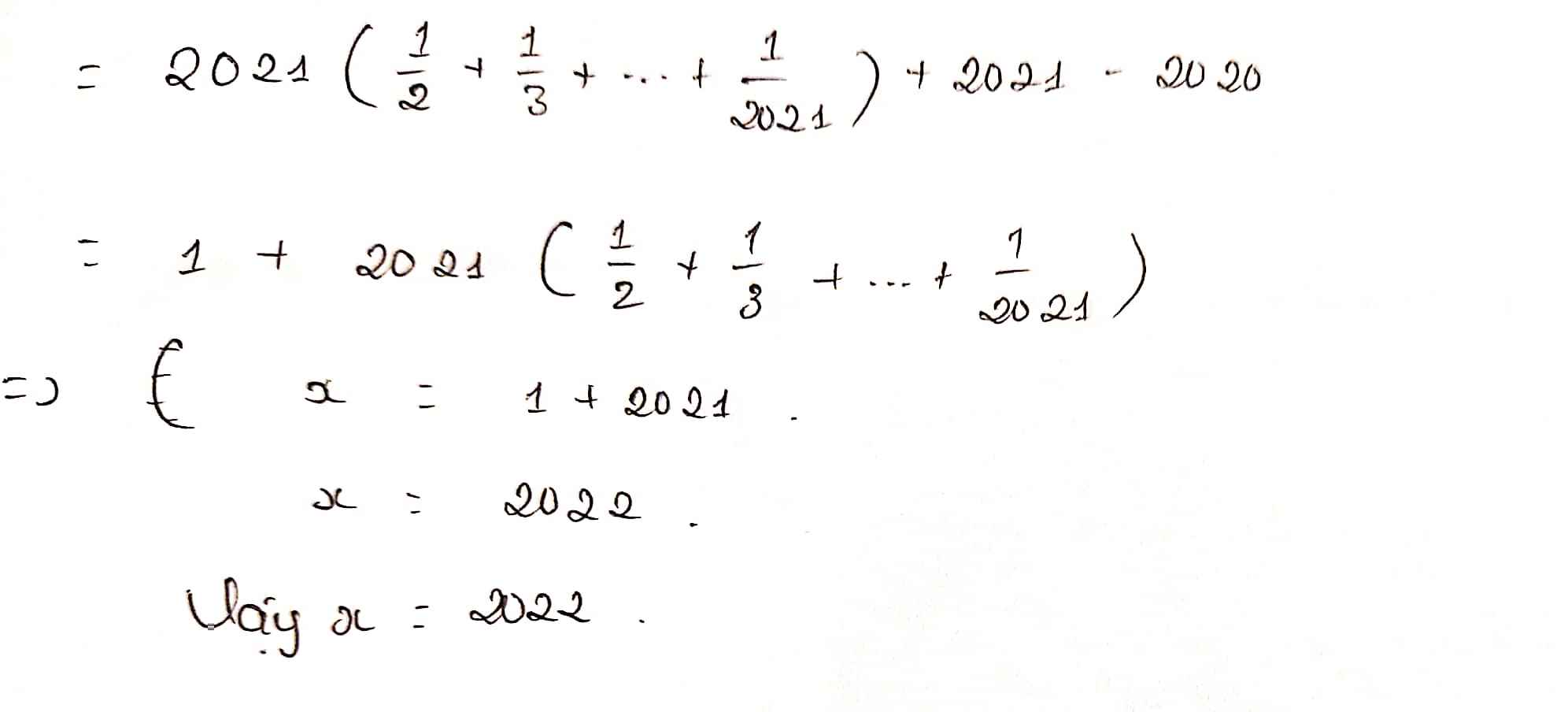
Ta có:
- các cơ số tận cùng là 0a0a tận cùng là 0
- các cơ số tận cùng là 1111 tận cùng là 1
- các cơ số tận cùng là 2222 tận cùng là 4
- các cơ số tận cùng là 3333 tận cùng là 7
- các cơ số tận cùng là 4444 tận cùng là 6
- các cơ số tận cùng là 5555 tận cùng là 5
- các cơ số tận cùng là 6666 tận cùng là 6
- các cơ số tận cùng là 7777 tận cùng là 3
- các cơ số tận cùng là 8888 tận cùng là 6
- các cơ số tận cùng là 9999 tận cùng là 9
=> Tổng của chúng là:
0+1+4+7+6+5+6+3+6+9=(...7)0+1+4+7+6+5+6+3+6+9=(...7)
Có tất cả số số hạng là:
(2021−1):1+1=2021(2021-1):1+1=2021 (số)
Có tất cả các nhóm số hạng từ cơ số tận cùng 1 - 0 là:
(2021−1):10=202(2021-1):10=202 (nhóm)
⇒(...7).202+(...1)=(....5)⇒(...7).202+(...1)=(....5)
Vậy số tận cùng của S là 5
-----------------------------------
Phần giải thích:
- Tại sao lại có −1-1 ở (2021−1):10=202(2021-1):10=202
+ Vì số 2021 thừa ra ngoài nên trừ đi.
- Tại sao lại có + (...1) ở ⇒(...7).202+(...1)⇒(...7).202+(...1)
+ Vì lúc đầu loại số 2021 tận cùng là 1 thì phải cộng lại nó vào