Cho phân số a/b > 0 , chứng minh rằng a/b + b/a > 2 .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HH
1
22 tháng 6 2021
Để \(\dfrac{a}{b}+\dfrac{b}{a}\ge2\)
<=> \(\dfrac{a}{b}+\dfrac{b}{a}-2\ge0\)
<=> \(\dfrac{a^2-2ab+b^2}{ab}\ge0\)
<=> \(\dfrac{\left(a-b\right)^2}{ab}\ge0\)
Mà \(\left(a-b\right)^2\ge0\)
\(\dfrac{a}{b}>0\) <=> ab > 0
=> đpcm
Dấu "=" xảy ra <=> a = b
DT
2
7 tháng 4 2017
Thiếu đề thì phải
Nhìn đề hình như là zầy phải k
\(\frac{a}{b}>0\)chứng minh \(\frac{a}{b}+\frac{b}{a}\ge\)số nào đó
Sửa để đi
7 tháng 4 2017
ta có: \(\frac{a}{b}>0\Rightarrow\frac{b}{a}>0\Rightarrow\frac{a}{b}+\frac{b}{a}\)>_ 0
BB
1
AH
Akai Haruma
Giáo viên
29 tháng 11 2023
Lời giải:
$a^4-4a=b^4-4b$
$\Leftrightarrow (a^4-b^4)-(4a-4b)=0$
$\Leftrightarrow (a-b)(a+b)(a^2+b^2)-4(a-b)=0$
$\Leftrightarrow (a-b)[(a+b)(a^2+b^2)-4]=0$
$\Rightarrow (a+b)(a^2+b^2)-4=0$ (do $a-b\neq 0$ với mọi $a,b$ phân biệt)
$\Rightarrow (a+b)(a^2+b^2)=4>0$
Mà $a^2+b^2>0$ với mọi $a,b$ phân biệt nên $a+b>0$
Mặt khác:
Áp dụng BĐT AM-GM:
$4=(a+b)(a^2+b^2)\geq (a+b).\frac{(a+b)^2}{2}$
$\Rightarrow 8> (a+b)^3$
$\Rightarrow 2> a+b$
Vậy $0< a+b< 2$
Ta có đpcm.
CM
2 tháng 6 2019
Ta có: (-a) . b = - (a . b) = a . (-b).
Do đó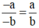 
(theo định nghĩa SGK).
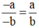(theo định nghĩa SGK).
CM
8 tháng 2 2017
Ta có: (-a) . b = - (a . b) = a . (-b).
Do đó 
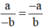(theo định nghĩa SGK).
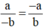(theo định nghĩa SGK).
Ta có: \(\left(a-b\right)^2\ge0\Leftrightarrow a^2-2ab+b^2\ge0\Leftrightarrow a^2+b^2\ge2ab\)
\(\frac{a}{b}+\frac{b}{a}=\frac{a^2+b^2}{ab}\ge\frac{2ab}{ab}=2\)
Dấu \(=\)xảy ra khi \(a=b\).