Tìm x, y nguyên biết: xy – 3y + x = 16 ...
Đọc tiếp
Tìm x, y nguyên biết: xy – 3y + x = 16
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
23 tháng 12 2022
Lời giải:
$xy+3x+3y=-16$
$(xy+3x)+(3y+9)=-7$
$x(y+3)+3(y+3)=-7$
$(y+3)(x+3)=-7$
Vì $x,y$ nguyên nên $x+3, y+3$ nguyên. Ta có bảng sau: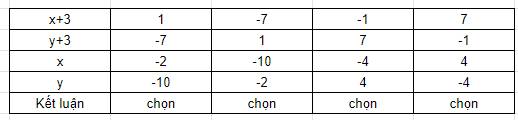
26 tháng 1 2018
a, Vì |2x+8| và |3y-9x| đều >= 0
=> |2x+8| + |3y-9x| >= 0
Dấu "=" xảy ra <=> 2x+8=0 và 3y-9x=0 <=> x=-4 và y=-12
Vậy x=-4 và y=-12
Tk mk nha
AH
Akai Haruma
Giáo viên
18 tháng 12 2021
Lời giải:
$x+3y+xy=5$
$(x+xy)+3y=5$
$x(y+1)+3(y+1)=8$
$(x+3)(y+1)=8$
Đến đây là dạng PT tích cơ bản. Bạn chỉ cần xét TH:
| x+3 | 1 | 8 | -1 | -8 | 2 | 4 | -2 | -4 |
| y+1 | 8 | 1 | -8 | -1 | 4 | 2 | -4 | -2 |
| x | -2 | 5 | -4 | -11 | -1 | 1 | -5 | -7 |
| y | 7 | 0 | -9 | -2 | 3 | 1 | -5 | -3 |
10 tháng 1 2017
xy + 3y - y = 6
xy + 2y = 6
y(x + 2) = 6.Ta có bảng sau :
| y | -6 | -3 | -2 | -1 | 1 | 2 | 3 | 6 |
| x + 2 | -1 | -2 | -3 | -6 | 6 | 3 | 2 | 1 |
| x | -3 | -4 | -5 | -8 | 4 | 1 | 0 | -1 |
Vậy (x ; y) = (-3 ; -6) ; (-4 ; -3) ; (-5 ; -2) ; (-8 ; -1) ; (4 ; 1) ; (1 ; 2) ; (0 ; 3) ; (-1 ; 6)
10 tháng 1 2017
Ta có : xy + 3y - y = 6
<=>y(x + 3 - 1) = 6
<=> y(x + 2) = 6
=> y và x + 2 thuộc ước của 6 là - 6 ;- 3 ;- 2 ;- 1 ;1 ;2 ;3 ;6
Nếu x + 2 = - 6 thì y = - 1 => x = - 8 thì y = - 1
x + 2 = - 3 thì y = - 2 => x = - 5 thì y = - 2
..................... (tự liệt kê tiếp nhé)
Vậy ..............
MS
1
MN
11 tháng 2 2016
1)2x+3y+xy=5
=>x(2+y)+3y=5
=>x(2+y)+3y+6=5+6
=>x(2+y)+3(2+y)=11
=>(x+3)(2+y)=11
=>(x+3) và (2+y) thuộc Ư(11)={-1;1;-11;11}
Ta có bảng sau:
x+3 -1 -11 1 11
2+y -11 -1 11 1
x -4 -14 -2 8
y -13 -3 9 -1
Vậy các cặp (x,y) cần tìm thỏa mãn đề bài là: (-4; -13); (-14; -3); (-2; 9); (8; -1)
2)xy+2x+2y=-16
=>x(2+y)+2y=-16
=>x(2+y)+2y+4=-16+4
=>x(2+y)+2.(2+y)=-12
=>(2+y)(x+2)=-12
=>(2+y) và (x+2) thuộc Ư(-12)={-1;1;-2;2;-3;3;-4;4;-6;6;-12;12}
Ta có bảng sau:
2+y -1 -12 -2 -6 -3 -4
x+2 -12 -1 -6 -2 -4 -3
y -3 -14 -4 -8 -5 -6
x -14 -3 -8 -4 -6 -5
Vậy các cặp số(x,y) cần tìm thỏa mãn đề bài là : (-14; -3); (-3; -14); (-8; -4); (-4; -8); (-6; -5); (-5; -6)
13 tháng 2 2018
\(xy-x-3y=2\)
\(\Leftrightarrow\left(xy-x\right)-\left(3y-3\right)=5\)
\(\Leftrightarrow x\left(y-1\right)-3\left(y-1\right)=5\)
\(\Leftrightarrow\left(x-3\right)\left(y-1\right)=5\)
Dễ rồi tự giải tiếp nhé
DT
0
26 tháng 2 2023
=>x(y-2)+3y-6=15
=>(y-2)(x+3)=15
=>\(\left(x+3;y-2\right)\in\left\{\left(1;15\right);\left(15;1\right);\left(-1;-15\right);\left(-15;-1\right);\left(3;5\right);\left(5;3\right);\left(-3;-5\right);\left(-5;-3\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(-2;17\right);\left(12;3\right);\left(-4;-13\right);\left(-18;1\right);\left(0;7\right);\left(2;5\right);\left(-6;-3\right);\left(-8;-1\right)\right\}\)
VN
4
31 tháng 8 2023
a) \(x\left(y-7\right)+y-12=0\left(x;y\inℤ\right)\)
\(\Rightarrow x\left(y-7\right)+y-7-5=0\)
\(\Rightarrow\left(x+1\right)\left(y-7\right)=5\)
\(\Rightarrow\left(x+1\right);\left(y-7\right)\in U\left(5\right)=\left\{-1;1;-5;5\right\}\)
\(\Rightarrow\left(x;y\right)\in\left\{\left(-2;2\right);\left(0;12\right);\left(-6;6\right);\left(4;8\right)\right\}\)
KV
31 tháng 8 2023
b) xy - 6x - 4y + 13 = 0
x(y - 6) - 4y + 24 - 11 = 0
x(y - 6) - 4(y - 6) = 11
(y - 6)(x - 4) = 11
TH1: x - 4 = 1 và y - 6 = 11
*) x - 4 = 1
x = 5
*) y - 6 = 11
y = 17
TH2: x - 4 = -1 và y - 6 = -11
*) x - 4 = -1
x = 3
*) y - 6 = -11
y = -5
TH3: x - 4 = 11 và y - 6 = 1
*) x - 4 = 11
x = 15
*) y - 6 = 1
y = 7
TH4: x - 4 = -11 và y - 6 = -1
*) x - 4 = -11
x = -7
*) y - 6 = -1
y = 5
Vậy ta có các cặp giá trị (x; y) sau:
(-7; 5); (15; 7); (3; -5); (5; 17)
Ta có xy - 3y + x = 16
=> xy - 3y + x - 3 = 13
=> y(x - 3) + (x - 3) = 13
=> (y + 1)(x - 3) = 13
Lập bảng xét các trường hơp
Vậy các cặp (x;y) nguyên tìm được là (4 ; 12) ; (16 ; 0) ; (2;-14) ; (-10; -2)
\(xy-3y+x=16\)
\(\Leftrightarrow y\left(x-3\right)+x-3=13\)
\(\Leftrightarrow\left(x-3\right)\left(y+1\right)=13\)
Mà \(x,y\)nguyên nên ta có bảng giá trị sau: