Chứng minh rằng a0=1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
26 tháng 12 2022
a0 = a1-1 = \(\dfrac{a}{a}\) = 1 (đk a#0)
a0 = 1 (đpcm)
26 tháng 12 2022
a0 = a1-1 = \dfrac{a}{a}
a\(\dfrac{a}{a}\) = 1 (đk a#0)
a0 = 1 (đpcm)
1 tháng 12 2016
Gọi phương trình đã cho là f(x)
Giả sử x = t là nghiệm hữu tỷ của f(x) thì: f(x) = (x - t)Q(x)
f(0) = a0 = - t.Q(x) (1)
Và f(1) = a2k + a2k-1 + ... + a1 + a0 = (1 - t).Q(x) (2)
Từ (1) ta có a0 là số lẻ nên t phải là số lẻ
Từ (2) ta thấy rằng a2k + a2k-1 + ... + a1 + a0 là tổng của 2k + 1 số lẻ nên là số lẻ. Từ đó ta thấy rằng (1 - t) là số lẻ
Mà (1 - t) là hiệu hai số lẻ nên không thể là số lẻ (mâu thuẫn)
Vậy f(x) không có nghiệm nguyên
28 tháng 7 2016
\(\left(x-a\right)\left(x+a\right)=x^2-a^2\)
Ta có:
VT \(\Leftrightarrow x^2+ax-ax-a^2\)
\(\Leftrightarrow x^2-a^2\)
\(\Rightarrow\) VT=VP=\(x^2-a^2\)
T7
1
16 tháng 12 2021
\(a,f\left(\dfrac{3}{2}\right)=2\cdot\dfrac{3}{2}=3\\ b,f\left(a\right)+f\left(-a\right)=2a-2a=0\)
22 tháng 9 2021
a) \(\frac{a}{a+b}=\frac{c}{c+d}\)=> a . ( c + d ) = c . ( a + b )
=> ac + ad = ac + cb
=> ad = bc
=> \(\frac{a}{b}=\frac{c}{d}\)
13 tháng 8 2015
b/ ta có: Góc DAE = 360 - (90 . 2) - góc A = 180 - 110 = 70 độ
từ tam giác ABM = tam giác KCM => AB = CK
Xét tam giác CAK & tam giác AED có:
KCA = DAE (bằng 70 độ)
AD = CK (bằng AB)
AC = AE (gt)
=> tam giác CAK = tam giác AED (cgc)
28 tháng 1 2016
b, vì tam giác ABM=tam giác KCM(câu a) =>AB=CK(2 cạnh tương ứng)
mà AB=AD(gt) =>KC=AD
Có DAE+DAB+EAC+BAC=3600=>DAE=3600-(DAB+EAC+BAC)
mả DAB=900(AD vuông góc vs AB-GT)
EAC=900(AE vuông góc vs AC-GT)
BAC=1100 (GT)
=>DAE=3600-(900+900+1100)=700
Có DAE=700(CMT)
ACK=700(câu a)
=>DAE=ACK(=700)
Xét tam giác CAK & tam giác AED có:
CK=AD(cmt)
CA=AE(gt)
DAE=ACK(cmt)
=>tam giác CAK=tam giác AED(c.g.c)
phần c mik k bit lm giúp nhé
CM
30 tháng 9 2019
Đáp án A
Ta có: 1 + x + x 2 n = 1 + x 1 + x n = ∑ k = 0 n C k n x k 1 + x k
= ∑ k = 0 n C n k x k ∑ j = 0 k C j k x k ⇒ T k + 1 = C k n x k ∑ j = 0 k C j k x k
Ta tính các số hạng như sau:
T 0 = 1 ;
T 1 = C n 1 C n 2 x + C n 1 C 1 1 x 2 = n x ; T 2 = C n 2 C n 0 x 2 + C n 2 C 2 1 x 3 + C n 2 C 2 2 x 4 , ....
Như vậy ta có:
a 3 = C n 2 C 2 1 + C n 3 C 2 0 ; a 4 = C n 2 C 2 2 + C n 3 C 3 1 + C n 4 C 4 0
Theo giả thiết
a 3 14 = a 4 41 ⇒ C n 2 C 2 1 + C n 3 C 2 0 14 = C n 2 C 2 2 + C n 3 C 3 1 + C n 4 C 4 0 41
⇔ 2. n n − 1 2 ! + n n − 1 n − 2 3 ! 14 = n n − 1 2 ! + 3 n n − 1 n − 2 3 ! + n n − 1 n − 2 n − 3 4 ! 41
⇔ 21 n 2 − 99 n − 1110 = 0 ⇒ n = 10
Trong khai triển:
1 + x + x 2 10 = a 0 + a 1 x + a 2 x 2 + ... + a 20 x 20
cho x = 1 ta được: S = a 0 + a 1 + a 2 + ... + a 20 = 3 10
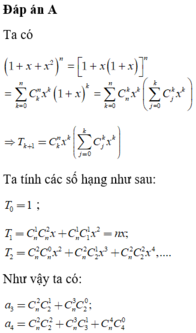
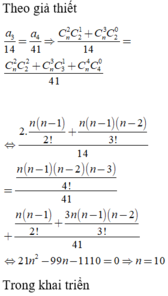
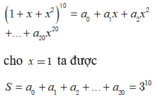
bổ sung: \(a\ne0\)