Cho a/b = b/c = c/a và a+b+c không bằng 0 ; a= 2015
Tính b và c ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 12 2019
Áp dụng tính chất dãy tỷ số bằng nhau ta đc\(\frac{-a+b+c}{a}=\frac{a-b+c}{b}=\)\(\frac{a+b-c}{c}=\frac{a+b+c}{a+b+c}=1\)
Dễ dàng cm đc \(a=b=c\)tính đc P=8
CM
2 tháng 10 2017
Có I(4;-2;1) là trung điểm AC. Ta có hệ điều kiện:
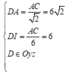
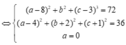
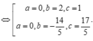
Đối chiếu điều kiện a ; b ; c ∈ ℤ ⇒ a = 0 , b = 2 , c = 1 và a+b+c=0+2+1=3
Chọn đáp án D.
NN
1
1 tháng 1 2020
Câu hỏi của nguyen thanh chuc - Toán lớp 7 - Học toán với OnlineMath
LN
1
1 tháng 1 2020
Câu hỏi của nguyen thanh chuc - Toán lớp 7 - Học toán với OnlineMath
FF
28 tháng 8 2016
3. abc > 0 nên trog 3 số phải có ít nhất 1 số dương.
Vì nếu giả sử cả 3 số đều âm => abc < 0 => trái giả thiết
Vậy nên phải có ít nhất 1 số dương
Không mất tính tổng quát, giả sử a > 0
mà abc > 0 => bc > 0
Nếu b < 0, c < 0:
=> b + c < 0
Từ gt: a + b + c < 0
=> b + c > - a
=> (b + c)^2 < -a(b + c) (vì b + c < 0)
<=> b^2 + 2bc + c^2 < -ab - ac
<=> ab + bc + ca < -b^2 - bc - c^2
<=> ab + bc + ca < - (b^2 + bc + c^2)
ta có:
b^2 + c^2 >= 0
mà bc > 0 => b^2 + bc + c^2 > 0
=> - (b^2 + bc + c^2) < 0
=> ab + bc + ca < 0 (vô lý)
trái gt: ab + bc + ca > 0
Vậy b > 0 và c >0
=> cả 3 số a, b, c > 0
3 tháng 5 2019
1.a, Ta có: \(\left(a+b\right)^2\ge4a>0\)
\(\left(b+c\right)^2\ge4b>0\)
\(\left(a+c\right)^2\ge4c>0\)
\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64abc\)
Mà abc=1
\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\left(đpcm\right)\)
