Cho hàm số f(x) có đạo hàm liên tục trên [ 0;1 ] và thỏa mãn ∫ 0 1 x f ' x - 2 d x = f 1 .Tính giá trị của I = ∫ 0 1 f x d x
A. -1
B. 1
C. 0
D. π
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
thỏa mãn
x
2
f
'
x
+
f
x
=
0
và
f
x
≠
0
,
∀
x
∈
0
;
+
∞
. Tính f(2) biết f(1) = e.
. 
CM
27 tháng 12 2018
Đáp án C.
Đặt u = f ( x ) d v = x + 1 e x d x ⇔ d u = f ' x d x v = x e x , khi đó ∫ 0 1 x + 1 e x . f x d x
= x e x . f x 0 1 - ∫ 0 1 x e x . f ' x d x
= e . f 1 - ∫ 0 1 x e x . f ' x d x ⇔ ∫ 0 1 x e x . f ' x d x = - ∫ 0 1 x + 1 e x . f x d x = 1 - e 2 4 .
Xét tích phân ∫ 0 1 f ' x + k . x e x 2 d x = ∫ 0 1 f ' x 2 d x + 2 k . ∫ 0 1 x e x . f ' x d x + k 2 . ∫ 0 1 x 2 e 2 x d x = 0
⇔ e 2 - 1 4 + 2 k . 1 - e 2 4 + k 2 . e 2 - 1 4 = 0 ⇒ k 2 - 2 k + 1 = 0 ⇔ k = 1 ⇒ f ' x = - x . e x .
Do đó f x = ∫ f ' x d x = - ∫ x . e x d x = 1 - x e x + C mà f 1 = 0 ⇒ C = 0 .
Vậy I = ∫ 0 1 f ( x ) d x = ∫ 0 1 ( 1 - x ) e x d x → c a s i o I = e - 2 .
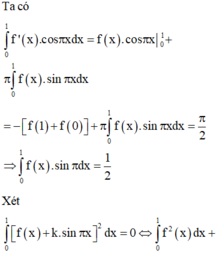
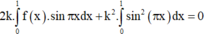
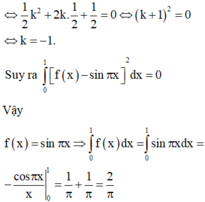
Áp dụng công thức tích phân từng phần, ta có
∫ 0 1 x f ' x - 2 d x = f x ⇒ ∫ 0 1 x f ' x d x = ∫ 0 1 2 x d x + f 1 ⇒ ∫ 0 1 x d f x = x 2 0 1 + f 1 = 1 + f 1 ⇒ x f x 0 1 - ∫ 0 1 f x d x = 1 + f 1 ⇒ ∫ 0 1 f x d x = - 1
Đáp án A