Trong không gian Oxyz, cho hai điểm A(10;6;-2), B(5;10;-9) và mặt phẳng Điểm M di động trên mặt phẳng sao cho MA, MB luôn tạo với các góc bằng nhau. Biết rằng M luôn thuộc một đường tròn cố định. Hoành độ của tâm đường tròn bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Ta có:
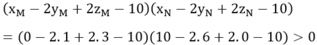
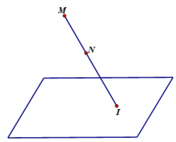
Nên hai điểm M và N nằm cùng phía so với mặt phẳng (P)
Ta luôn có: ![]() , nên |IM - IN| lớn nhất khi và chỉ khi I là giao điểm của đường thẳng MN với mặt phẳng (P).
, nên |IM - IN| lớn nhất khi và chỉ khi I là giao điểm của đường thẳng MN với mặt phẳng (P).
Đường thẳng MN có vec-tơ chỉ phương ![]() , nên phương trình đường thẳng MN là:
, nên phương trình đường thẳng MN là: 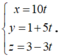
Tọa độ giao điểm I của đường thẳng MN với mặt phẳng (P) ứng với t là nghiệm phương trình:
10t - 2(1+5t) + 2(3-3t) - 10 = 0 <=> t = -1
Do đó I (-10; -4; 6), từ đó ta có a = -4 và b = 6, nên T = -4 + 6 = 2.

Đáp án C.
![]()
![]()
suy ra M,N cùng phía so với (P).
Do đó I M - I N ≤ M N Dấu bằng xảy ra khi I là giao điểm của MN và (P).
Phương trình đường thẳng MN là
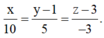
![]()
![]()
=> t = -1
![]()
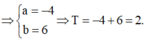
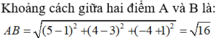
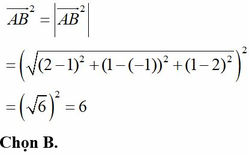
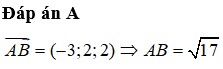
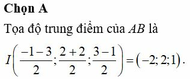


Đáp án B
Phương pháp:
+) Gọi M(x;y;z) tọa độ các véc tơ A M → , B M →
+) Gọi H, K lần lượt là hình chiếu của A,B lên ( α ) , có AMH = BMK
+) Tính sin các góc AMH = BMK và suy ra đẳng thức. Tìm quỹ tích điểm M là một đường tròn.
+) Tính tâm của đường tròn quỹ tích đó.
Cách giải:
Gọi M(x;y;z)
Gọi H, K lần lượt là hình chiếu của A, B lên ( α ) có AMH = BMK
= 3
Khi đó
Suy ra
Vậy M ∈ (C) là giao tuyến của ( α ) và (S). Tâm K của (C) là hình chiếu của
I 10 3 ; 34 3 ; - 34 3 trên mặt phẳng ( α ) .
Phương trình đương thẳng đi qua I và vuông góc với ( α ) có dạng