
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

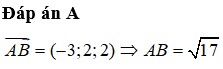

Đáp án D
Mặt phẳng cần tìm sẽ vuông góc với (ABM). Một vecto pháp tuyến của nó là tích có hướng của vecto pháp tuyến mặt phẳng (ABM) và A B →
Cũng có thể làm như sau: Khoảng cách lớn nhất là MH với H là hình chiếu vuông góc của M lên đường thẳng AB. Ta tìm được H ( 3 ; − 3 ; − 10 ) .

Đáp án B
Phương pháp:
Từ các giả thiết đã cho, lập hệ 3 phương trình ba ẩn a, b, c.
Giải hệ phương trình tìm a, b, c và tính tổng S.
Cách giải:
M ∈ P ⇒ 2 a − b + c + 1 = 0 A B → = − 2 ; 4 ; − 16 ; A M → = a + 1 ; b − 3 ; c + 2
⇒ A B → ; A M → = ( 16 b + 4 c − 40 ; − 16 a + 2 c − 12 ; − 4 a − 2 b + 2 )
n → P = 2 ; − 1 ; 1
⇒ 2 16 b + 4 c − 40 − − 16 a + 2 c − 12 + − 4 a − 2 b + 2 = 0
Ta có
⇔ 12 a + 30 b + 6 c = 66 ⇔ 2 a + 5 b + c = 11
M A 2 + M B 2 = 246
⇔ a + 1 2 + b − 3 2 + c + 2 2 + a + 3 2 + b − 7 2 + c + 18 2 = 246
⇔ a 2 + b 2 + c 2 + 4 a − 10 b + 20 c + 75 = 0
Khi đó ta có hệ phương trình
2 a − b + c = − 1 1 2 a + 5 b + c = 11 2 a 2 + b 2 + C 2 + 4 a − 10 b + 20 c + 75 = 0 3


Kiểm tra thấy A và B nằm khác phía so với mặt phẳng (P)
Ta tìm được điểm đối xứng với B qua (P) là B ' ( -1;-3;4 )
Lại có M A - M B = M A - M B ' ≤ A B ' = c o n s t .
Vậy M A - M B đạt giá trị lớn nhất khi M, A, B’ thẳng hàng hay M là giao điểm của đường thẳng AB’ với mặt phẳng (P).
Đường thẳng AB’ có phương trình tham số là x = 1 + t y = - 3 z = - 2 y .
Tọa độ điểm M ứng với tham số t là nghiệm của phương trình
1 + t + - 3 + - 2 t - 1 = 0 ⇔ t = - 3 ⇒ M - 2 ; - 3 ; 6
Suy ra a = -2; b = -3; c = 6
Vậy a + b + c = 1
Đáp án A