Cho hình thang ABCD (đáy lớn CD), gọi O là giao điểm của AC và BD; các đường kẻ từ A và B lần lượt song song với BC và AD cắt các đường chéo BD và AC tương ứng ở F và E. Chứng minh:
a) EF // AB
b) 2AB = EF . CD
c) Gọi S1 ;S2 ;S3 ;S4 theo thứ tự là diện tích của các tam giác OAB; OCD; OAD và OBC
Chứng minh: S1 . S2 = S3 . S4


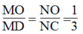
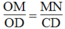 Hệ quả định lí Ta-lét)
Hệ quả định lí Ta-lét)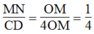
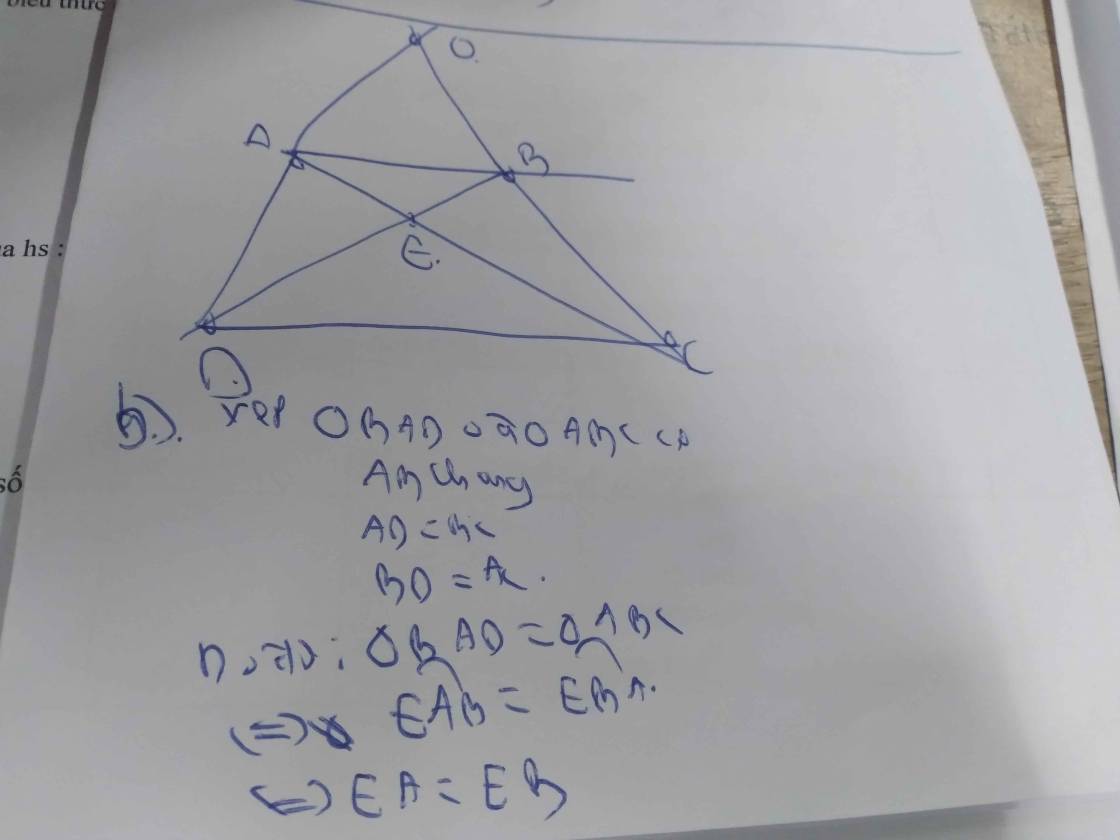

A B C D O F E
a) Do AF//BC nên áp dụng hệ quả định lý Talet ta có: \(\frac{OF}{OB}=\frac{AO}{OC}\)
Tương tự ta có: \(\frac{OE}{OA}=\frac{OB}{OD}\) mà AB // CD nên \(\frac{OB}{OA}=\frac{OA}{OC}\)
Từ đó suy ra \(\frac{OE}{OA}=\frac{OF}{OB}\Rightarrow\) EF // AB.
b) Do AB // EF nên \(\frac{EF}{AB}=\frac{OF}{OB}=\frac{OA}{OC}=\frac{AB}{CD}\Rightarrow\frac{EF}{AB}=\frac{AB}{CD}\Rightarrow AB^2=EF.CD\)
c) Ta thấy tam giác OAB và OBC chung chiều cao hạ từ đỉnh B nên \(\frac{S_{OAB}}{S_{OBC}}=\frac{OA}{OC}\Rightarrow\frac{S_1}{S_4}=\frac{OA}{OC}\)
Tam giác OAD và ODC chung chiều cao hạ từ đỉnh D nên \(\frac{S_{OAD}}{S_{ODC}}=\frac{OA}{OC}\Rightarrow\frac{S_3}{S_2}=\frac{OA}{OC}\)
Vậy thì \(\frac{S_1}{S_4}=\frac{S_3}{S_2}\Rightarrow S_1.S_2=S_3.S_4\left(đpcm\right)\)
ABCDOFE
a) Do AF//BC nên áp dụng hệ quả định lý Talet ta có: OFOB =AOOC
Tương tự ta có: OEOA =OBOD mà AB // CD nên OBOA =OAOC
Từ đó suy ra OEOA =OFOB ⇒ EF // AB.
b) Do AB // EF nên EFAB =OFOB =OAOC =ABCD ⇒EFAB =ABCD ⇒AB2=EF.CD
c) Ta thấy tam giác OAB và OBC chung chiều cao hạ từ đỉnh B nên SOABSOBC =OAOC ⇒S1S4 =OAOC
Tam giác OAD và ODC chung chiều cao hạ từ đỉnh D nên SOADSODC =OAOC ⇒S3S2 =OAOC
Vậy thì S1S4 =S3S2 ⇒S1.S2=S3.S4(đpcm)