Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

M,N lần lượt là trung điểm của SB và SB là sai đề rồi bạn. Bạn coi lại đề nha

a: \(I\in BD\subset\left(SBD\right)\)
\(I\in AC\subset\left(SAC\right)\)
Do đó: \(I\in\left(SBD\right)\cap\left(SAC\right)\)
mà \(S\in\left(SBD\right)\cap\left(SAC\right)\)
nên \(\left(SBD\right)\cap\left(SAC\right)=SI\)
b: Gọi K là giao của AB và CD
\(K\in AB\subset\left(SAB\right)\)
\(K\in CD\subset\left(SCD\right)\)
Do đó: \(K\in\left(SAB\right)\cap\left(SCD\right)\)
mà \(S\in\left(SAB\right)\cap\left(SCD\right)\)
nên \(\left(SAB\right)\cap\left(SCD\right)=SK\)
c: AD//BC
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
Do đó: \(\left(SAD\right)\cap\left(SBC\right)=xy\), xy đi qua S và xy//AD//BC

Hình câu c là tui vẽ riêng ra cho dễ nhìn thôi, còn hình vẽ trình bày vô bài lấy hình chung ở câu a và b nhó :v



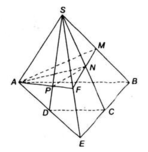
a) Tìm (SAD) ∩ (SBC)
Gọi E= AD ∩ BC. Ta có:
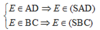
Do đó E ∈ (SAD) ∩ (SBC).
mà S ∈ (SAD) ∩ (SBC).
⇒ SE = (SAD) ∩ (SBC)
b) Tìm SD ∩ (AMN)
+ Tìm giao tuyến của (SAD) và (AMN) :
Trong mp (SBE), gọi F = MN ∩ SE :
F ∈ SE ⊂ (SAD) ⇒ F ∈ (SAD)
F ∈ MN ⊂ (AMN) ⇒ F ∈ (AMN)
⇒ F ∈ (SAD) ∩ (AMN)
⇒ AF = (SAD) ∩ (AMN).
+ Trong mp (SAD), gọi AF ∩ SD = P
⇒ P = SD ∩ (AMN).
c) Tìm thiết diện với mp(AMN):
(AMN) ∩ (SAB) = AM;
(AMN) ∩ (SBC) = MN;
(AMN) ∩ (SCD) = NP
(AMN) ∩ (SAD) = PA.
⇒ Thiết diện cần tìm là tứ giác AMNP.

a: \(E\in AC\subset\left(SAC\right)\)
\(E\in BD\subset\left(SBD\right)\)
Do đó: \(E\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SE\)
b: Gọi K là giao của AD với BC
\(K\in AD\subset\left(SAD\right)\)
\(K\in BC\subset\left(SBC\right)\)
Do đó: \(K\in\left(SAD\right)\cap\left(SBC\right)\)
mà \(S\in\left(SAD\right)\cap\left(SBC\right)\)
nên \(SK=\left(SAD\right)\cap\left(SBC\right)\)
c: AB//CD
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
Do đó: \(\left(SAB\right)\cap\left(SCD\right)=xy\), xy đi qua S và xy//AB//CD

a: \(E\in AC\subset\left(SAC\right);E\in BD\subset\left(SBD\right)\)
=>\(E\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SE\)
b: Gọi K là giao của AD và BC
\(K\in AD\subset\left(SAD\right);K\in BC\subset\left(SBC\right)\)
=>\(K\in\left(SAD\right)\cap\left(SBC\right)\)
mà \(S\in\left(SAD\right)\cap\left(SBC\right)\)
nên \(\left(SAD\right)\cap\left(SBC\right)=SK\)
c: Xét (SAB) và (SCD) có
AB//CD
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
Do đó: (SAB) giao (SCD)=xy; xy đi qua S và xy//AB//CD

a: Ta có: CD//AB
AB\(\subset\)(SAB)
CD không nằm trong mp(SAB)
Do đó: CD//(SAB)
b: Xét ΔSBD có
M,N lần lượt là trung điểm của SB,SD
=>MN là đường trung bình của ΔSBD
=>MN//BD
Xét (CMN) và (ABCD) có
\(C\in\left(CMN\right)\cap\left(ABCD\right)\)
MN//BD
Do đó: (CMN) giao (ABCD)=xy, xy đi qua C và xy//MN//BD