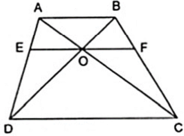
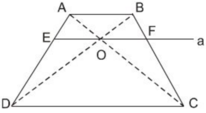
Cho hình thang ABCD (AB // CD) , hai đường chéo cắt nhau tại O . Trên đáy CD lấy E và F sao cho OE // AD ; OF // BC . Chứng minh S ODE = S OCF .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


OE // AD => DE / CD = AO/AC (1)
OF // BC => FC / Dc = OB /BD (2)
Vì AB // DC => AO / OC = OB /OD
=> AO/(AO+OC) = OB/( OD+OB)
=> AO/AC = OB/ BD (3)
TỪ (1),(2),(3)
=> DE/CD = FC/CD
=> DE = FC (4)
từ o kẻ OH vuông DC
=> S ode = 1/2*DE*OH
S OCf = 1/2*FC*OH
Từ (4) => S ODE = S OCf (dpcm )
Vì \(OE//AD\)
\(\Rightarrow\frac{DE}{DC}=\frac{OA}{CA}\)(1)
\(OF//BC\)
\(\Rightarrow\frac{CF}{CD}=\frac{BO}{BD}\)(2)
\(AB//CD\)
\(\Rightarrow\frac{AO}{AC}=\frac{BO}{BD}\)(3)
Từ (1) ; (2) và (3)
\(\Rightarrow\frac{DE}{DC}=\frac{CF}{DC}\)
\(\Rightarrow DE=CF\)
Mà trong các tam giác ODE và OCF có 1 cặp cạnh = nhau , có cùng chiều cao hạ từ đỉnh O tới cặp cạnh đó nên
\(\Rightarrow S_{ODE}=S_{OFC}\)(đpcm)

Bạn tự vẽ hình nhé
Xét \(\Delta ACD\) có OE // CD(gt)
=> \(\dfrac{OE}{DC}=\dfrac{AO}{AC}\left(1\right)\)
Xét \(\Delta BCD\) có OF // CD (gt)
=> \(\dfrac{OF}{DC}=\dfrac{BF}{FC}\left(2\right)\)
Mặt khác AB // CD nên \(\dfrac{AO}{AC}=\dfrac{BF}{FC}\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\)
=> \(\dfrac{OE}{DC}=\dfrac{OF}{DC}\) => OE = OF

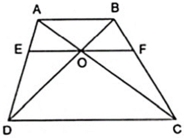
Tam giác ABD có OE//AB
=>DO/DB = OE/AB (Theo hệ quả Đlý Ta-lét) (1)
Tam giác ABC có OF//AB
=>CO/CA = OF/AB (Theo hệ quả Đlý Ta-lét) (2)
Tam giác ABO có CD//AB
=>OD/OB = OC/OA (Theo hệ quả Đlý Ta-lét)
=> OD/(OB+OD) = OC/(OA+OC) hay OD/DB=CO/CA (3)
Từ (1) (2) và (3)
=> OE/AB = OF/AB
=> OE = OF (đpcm.)

Áp dụng hệ quả của định lí Ta – lét cho OE//DC,
OF//DC và AB//DC ta được:
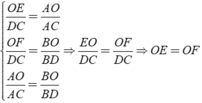
Điều phải chứng minh.

Áp dụng hệ quả của định lí Ta – lét cho OE//DC,
OF//DC và AB//DC ta được:
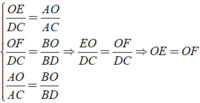
Điều phải chứng minh.

Bài 1:
Áp dụng định lý Talet cho $EO\parallel DC$:
$\frac{OE}{DC}=\frac{AO}{AC}(1)$
Áp dụng định lý Talet cho $OF\parallel DC$:
$\frac{OF}{DC}=\frac{OB}{BD}(2)$
Áp dụng định lý Talet cho $AB\parallel CD$:
$\frac{OA}{OC}=\frac{OB}{OD}\Leftrightarrow \frac{OA}{OA+OC}=\frac{OB}{OB+OD}\Leftrightarrow \frac{OA}{AC}=\frac{OB}{BD}(3)$
Từ $(1);(2);(3)\Rightarrow \frac{OE}{DC}=\frac{OF}{DC}$
$\Rightarrow OE=OF$ (đpcm)

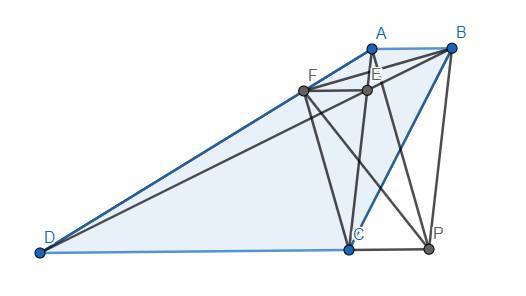
Dựng hình bình hành ABPC. Khi đó \(AD=AB+CD=CP+CD=DP\)
Ta có \(\dfrac{AB}{FE}=\dfrac{DA}{DF}\), \(\dfrac{CD}{FE}=\dfrac{DA}{AF}\)
\(\Rightarrow\dfrac{AB+CD}{FE}=DA\left(\dfrac{1}{DF}+\dfrac{1}{AF}\right)\)
\(\Rightarrow\dfrac{1}{FE}=\dfrac{DA}{DF.AF}\) \(\Rightarrow\dfrac{DF}{FE}=\dfrac{DP}{FA}\) \(\Rightarrow\dfrac{DF}{DC}=\dfrac{DP}{DA}=1\)
Từ đó \(\Delta DFC\) cân tại D. \(\Rightarrow\widehat{DFC}=\widehat{DCF}=\widehat{CFE}\) \(\Rightarrow\) FC là tia phân giác của \(\widehat{DFE}\). CMTT, FB là tia phân giác của \(\widehat{AFE}\). Do đó \(\widehat{BFC}=90^o\) (đpcm)



AB//CD theo Thales có:
\(\frac{OA}{OC}=\frac{OB}{OD}\Leftrightarrow\frac{OA}{OB}=\frac{OC}{OD}=\frac{OA+OC}{OB+OD}=\frac{AC}{BD}\Rightarrow\frac{OC}{AC}=\frac{OD}{BD}\left(1\right)\)
OE//AD nên \(\frac{OC}{AC}=\frac{CE}{CD}\left(2\right)\) và OF//BC nên \(\frac{OD}{BD}=\frac{DF}{DC}\left(3\right)\)
(1),(2) và (3) có: \(\frac{CE}{CD}=\frac{DF}{CD}\Rightarrow CE=DF\Leftrightarrow CF+EF=DE+EF\Leftrightarrow CF=DE\)
Suy ra \(S_{ODE}=S_{OCF}\) ( chung đỉnh nên cùng chiều cao và 2 đáy bằng nhau)
Xét ΔOCD có AB//CD (gt), theo đ/lí Ta-lét có: \(\frac{OA}{AC}=\frac{OB}{BD}\left(1\right)\)
Xét ΔADC có OE//AD (gt), theo đ/lí Ta-lét có: \(\frac{OA}{AC}=\frac{DE}{DC}\left(2\right)\)
Xét ΔBCD có OF//BC (gt), theo đ/lí Ta-lét có: \(\frac{OB}{BD}=\frac{CF}{CD}\left(3\right)\)
Từ (1), (2), (3) => \(\frac{DE}{CD}=\frac{CF}{CD}\) => DE = CF
=> SODE = SOCF (2 Δ có chung đường cao hạ từ O, đáy DE = CF)