Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C, trên tia Oy lấy hai điểm B, D sao cho OA = OB; OC = OD (A nằm giữa O và C; B nằm giữa O và D). So sánh hai góc CAD và CBD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 1 2024
Xét ΔODB và ΔOCA có
\(\dfrac{OD}{OC}=\dfrac{OB}{OA}\left(\dfrac{3}{6}=\dfrac{4}{8}\right)\)
\(\widehat{O}\) chung
Do đó: ΔODB đồng dạng với ΔOCA
=>\(\dfrac{OD}{OC}=\dfrac{OB}{OA}\)
=>\(\dfrac{OD}{OB}=\dfrac{OC}{OA}\)
Xét ΔODC và ΔOBA có
\(\dfrac{OD}{OB}=\dfrac{OC}{OA}\)
\(\widehat{O}\) chung
Do đó: ΔODC đồng dạng với ΔOBA
=>\(\dfrac{DC}{BA}=\dfrac{OC}{OA}\)
=>\(\dfrac{DC}{5}=\dfrac{6}{8}=\dfrac{3}{4}\)
=>\(DC=3\cdot\dfrac{5}{4}=\dfrac{15}{4}=3,75\left(cm\right)\)
3 tháng 12 2021
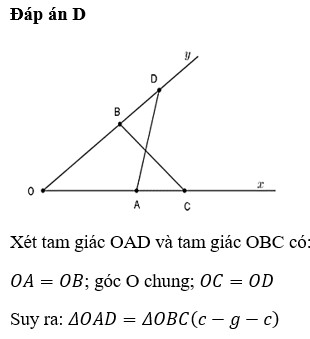
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
5 tháng 4 2020
a) Xét \(\Delta AOD\)và \(\Delta\)BOC có:
OA=OB (gt)
\(\widehat{O}\)chung
OD=OC (gt)
=> \(\Delta AOD=\Delta BOC\left(cgc\right)\)
=> AD=BC (2 cạnh tương ứng) (đpcm)
b) Ta có: \(\hept{\begin{cases}OC=OD\\OA=OB\end{cases}\Rightarrow OC-OA=OD-OB\Leftrightarrow AC=BD}\)
Xét tam giác EBD và tam giác EAC có:
AC chung
\(\widehat{DBE}=\widehat{CAE}\)
\(\widehat{BDE}=\widehat{ECA}\)
\(\Rightarrow\Delta EBD=\Delta EAC\left(gcg\right)\)
=> DE=EC (2 cạnh tương ứng)
Xét tam giác OED và tam giác OEC có:
OD=OC (gt)
OE chung
DE=EC (cmt)
=> \(\Delta OED=\Delta OEC\left(ccc\right)\)
=> \(\widehat{DOE}=\widehat{COE}\)(2 góc tương ứng)
=> OE là phân giác \(\widehat{xOy}\)(đpcm)
2 tháng 1 2022
x O y A B C D E
a) Xét ΔOBC và ΔOAD , có :
góc O chung
OB = OA ( gt )
OC = OD ( gt )
=> ΔOBC = ΔOAD ( c.g.c )
=> AD = BC ( 2 cạnh tương ứng ) ( đpcm )
=> góc OCB = góc ODA ( 2 góc tương ứng )
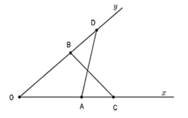
a) Xét ▲OAD và ▲OBC có :
OA = OB ( gt )
góc COD chung
OC = OD ( gt )
=> ▲OAD = ▲OBC ( c-g-c )
=> đpcm
b) Gọi giao điểm của BC và AD là M
Vì ▲OAD = ▲OBC ( c/m trên )
=> góc OCB = góc ODA ( 2 góc tương ứng )
Xét ▲ACM có góc MAC + góc ACM + góc CMA = 1800
Xét ▲BMD có góc BMD + góc MDB + góc DBM = 1800
Mà góc OCB = góc ODA ( c/m trên ) và góc CMA = góc BMD ( đối đỉnh )
=> góc CAM = góc MBD ( đpcm )
thanks