Cho \(\Delta ABC\)(AB>AC). Trên cạnh AB lấy điểm D sao cho AD=AC; Gọi E là trung điểm của CD. Tia AE cắt BC tại I.
1) Chứng minh: \(\Delta ADE=\Delta ACE\)
2) Chứng minh: DI = CI
3) Qua B vẽ vẽ đường thẳng song song với DC, cắt tia AC tại H. Chứng Minh AE\(\perp\)BH
4*) Chứng minh ba điểm D ; I ; H thẳng hàng
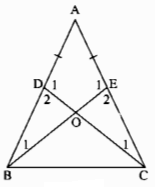
(Vẽ hình và viết giả thiết nha)

a, \(\text{Xét }\Delta ADE\text{ có }\)
\(AC=AD\)
\(\Rightarrow\Delta ADE\text{cân tại A}\)
Xét \(\Delta ADE\) cân tại A có:
AE là là đường trung tuyến ứng với cạnh đáy CD
\(\Rightarrow\)AE là đường cao\(\Rightarrow\widehat{AEC}=\widehat{AED}=90\)
Xét \(\Delta ADE\) và \(\Delta ACE\) có:
\(\widehat{AEC}=\widehat{AED}=90\)
AE chung
\(EC=ED\)
\(\Rightarrow\Delta ADE=\Delta ACE\) (cặp cạnh góc vuông)
b,Từ câu a, ta có:
\(\Delta ACD\) cân tại A
Mà AE là đường trung tuyến ứng với cạnh đáy CD
\(\Rightarrow\) AE là tia phân giác của \(\widehat{CAD}\) \(\Rightarrow\widehat{CAI}=\widehat{DAI}\) \(\left(1\right)\)
Xét \(\Delta ACI\) và \(\Delta ADI\) có:
AC=AD
\(\widehat{CAI}=\widehat{DAI}\) \(\text{ theo }\left(1\right)\)
\(AE\) chung
\(\Rightarrow\Delta ACI=\Delta ADI\) \(\left(c-g-c\right)\)
\(\Rightarrow DI=CI\)