Cho \(\Delta\)ABC góc A = 90 độ . Đoạn AB = AC . góc B = C = 45 độ . Gọi M ; E lần lượt là trung điểm đoạn BC và MC . Vẽ BH và CK vuông với AE . CMR :
a)BH=AK
b)\(\Delta MBH=\Delta MAK\)
GIÚP NHA ! MAI TÔI CẦN RỒI ! NHANH MÀ TÔI HIỂU SẼ ĐƯỢC TICK !
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 2 2023
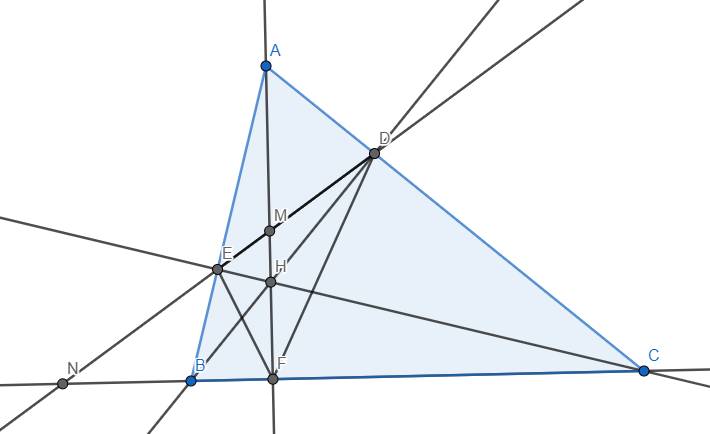
a) Xét \(\Delta ABD\) và \(\Delta ACE\), ta có \(\widehat{ADB}=\widehat{AEC}\left(=90^o\right)\) và góc A chung \(\Rightarrow\Delta ABD~\Delta ACE\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\) \(\Rightarrowđpcm\)
b) Từ \(AE.AB=AD.AC\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét \(\Delta ADE\) và \(\Delta ABC\), ta có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\) và góc A chung \(\Rightarrowđpcm\)
c) Do \(\Delta ADE~\Delta ABC\) \(\Rightarrow\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{AD}{AB}\right)^2\)
Lại có \(\dfrac{AD}{AB}=cosA=cos45^o=\dfrac{1}{\sqrt{2}}\) nên \(\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{1}{\sqrt{2}}\right)^2=\dfrac{1}{2}\)\(\Rightarrow\dfrac{S_{ADE}}{S_{ABC}-S_{ADE}}=\dfrac{1}{2-1}\) \(\Rightarrow\dfrac{S_{ADE}}{S_{BEDC}}=1\)
d) Kẻ đường cao AF của tam giác ABC. Tương tự câu b, ta chứng minh được các tam giác BFE và CDF cùng đồng dạng với tam giác ABC. Từ đó suy ra \(\Delta BEF~\Delta DCF\) \(\Rightarrow\widehat{BFE}=\widehat{CFD}\) \(\Rightarrow90^o-\widehat{BFE}=90^o-\widehat{CFD}\) \(\Rightarrow\widehat{EFM}=\widehat{DFM}\) \(\Rightarrow\) FM là tia phân giác trong tam giác DEF \(\Rightarrow\dfrac{MD}{ME}=\dfrac{FD}{FE}\).
Mặt khác, \(FN\perp FM\) \(\Rightarrow\) FN là phân giác ngoài của tam giác DEF \(\Rightarrow\dfrac{ND}{NE}=\dfrac{FD}{FE}\). Từ đó suy ra \(\dfrac{MD}{ME}=\dfrac{ND}{NE}\) \(\Rightarrowđpcm\)
12 tháng 12 2021
a: Xét ΔCIA và ΔDIB có
IC=ID
\(\widehat{CIA}=\widehat{DIB}\)
IA=IB
Do đó: ΔCIA=ΔDIB
16 tháng 3 2023
Kéo dài HN cắt đường vuông góc AB tại B ở Q
ΔBAI=ΔBHI(Cạnh huyền-góc nhọn)
=>BA=BH
mà AB=AN=BQ
nên BH=BQ=AN=AB
=>ΔBHN=ΔBQN
=>góc HBN=góc QBN
góc ABI=góc IBH
=>góc IBN=1/2*góc ABQ
=>góc IBN=45 độ
16 tháng 3 2021
a) Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)(BD là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABD=ΔHBD(cạnh huyền-góc nhọn)
Suy ra: BA=BH(Hai cạnh tương ứng)
28 tháng 1 2023
Xét tứ giác AEHD có
góc AEH+góc ADH=180 độ
=>AEHD là tứ giác nội tiếp
=>góc A+góc DHE=180 độ
9 tháng 5 2023
a: góc C<góc B
=>AB<AC
b: Xét ΔABM co AB=AM và góc A=60 độ
nên ΔAMB đều
hình tự vẽ nha bạn! ko có hình hơi khó hiểu có j thì cứ hỏi mình ^^
a) ta có: góc BAK+góc KAC=90 độ
góc ABH+ góc BAH (là góc BAK) =90 độ
=> góc ABH=góc KAC (cùng phụ góc BAK)
xét tam giác BHA vuông và tam giác KAC vuông (ch-gn)=> BH=AK
b) trong tam giác vuông cân ABC có AM là trung tuyến (M là tđ của BC)
=> AM là đường cao
=> góc AMC=90 độ
mà góc BHE =90'độ (tam giác BHA vuông tại H)
=> góc HBE=góc MAE (cùng phụ góc BEA)
ta có tam giác ABC vuông tại A có AM là t tuyến ứng v cạnh huyền BC
=> AM =1/2BC
mà BN=1/2BC
=> AM =BM
xét tam giác MBH và tam giác MAK (c-g-c)
Cám ơn kagamine rin len nha !