K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 8
Bài 6:
a: Xét tứ giác AMCK có
I là trung điểm chung của AC và MK
=>AMCK là hình bình hành
b: ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=MB=MC
Xét hình bình hành AMCK có MA=MC
nên AMCK là hình thoi
c: Ta có: AMCK là hình thoi
=>AK//CM và AK=CM
AK//CM
=>AK//MB
Ta có: AK=CM
CM=MB
Do đó; AK=MB
Xét tứ giác ABMK có
AK//MB
AK=MB
Do đó; ABMK là hình bình hành
d: Xét tứ giác ABEC có
M là trung điểm chung của AE và BC
=>ABEC là hình bình hành
Hình bình hành ABEC có AB=AC
nên ABEC là hình thoi
Bài 5:
a: Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
\(\hat{ADH}=\hat{CBK}\) (hai góc so le trong, AD//BC)
Do đó: ΔAHD=ΔCKB
b: ΔAHD=ΔCKB
=>HD=KB; AH=CK
ta có: AH⊥BD
CK⊥BD
Do đó:AH//CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành
c: Ta có: AH//CK
=>AM//CN
ta có: AB//CD
=>AN//CM
Xét tứ giác ANCM có
AN//CM
AM//CN
Do đó: ANCM là hình bình hành
d: Ta có; ANCM là hình bình hành
=>AC cắt NM tại trung điểm của mỗi đường(1)
Ta có:ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1),(2) suy ra AC,MN,BD đồng quy
Bài 2:
a: Ta có: \(AE=EB=\frac{AB}{2}\)
\(DF=FC=\frac{DC}{2}\)
mà AB=CD
nên AE=EB=DF=FC
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
b: Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
=>DE//BF
=>FN//EM
Ta có: AECF là hình bình hành
=>AF//CE
=>FM//EN
Xét tứ giác MENF có
ME//NF
MF//NE
Do đó: MENF là hình bình hành
c: Ta có: MENF là hình bình hành
=>MN cắt EF tại trung điểm của mỗi đường(1)
Ta có: AECF là hình bình hành
=>AC cắt EF tại trung điểm của mỗi đường(2)
Từ (1),(2) suy ra AC,EF,MN đồng quy
11 tháng 1 2023
a: Xét tứ giác DIHK có
góc DIH=góc DKH=góc KDI=90 độ
nên DIHK là hình chữ nhật
b: Xét tứ giác IHAK có
IH//AK
IH=AK
Do đó: IHAK là hình bình hành
=>B là trung điểm chung của IA và HK
Xét ΔIKA có IC/IK=IB/IA
nên BC//KA
Xét ΔIDA có IB/IA=IM/ID
nên BM//DA
=>B,C,M thẳng hàng
P
2
28 tháng 8
a:
b: TH1: \(\hat{BAD}>90^0;\hat{ABD}>90^0\)
Ta có: ABCD là hình thang
=>\(\hat{ABC}+\hat{BCD}=180^0\)
=>\(\hat{BCD}<180^0-90^0=90^0\)
=>\(\hat{BCD}<\hat{BAD}\)
TH2: \(\hat{ADC}>90^0;\hat{DCB}>90^0\)
Ta có: ABCD là hình thang
DC//AB
=>\(\hat{CDA}+\hat{DAB}=180^0\)
=>\(\hat{DAB}<180^0-90^0=90^0\)
=>\(\hat{DAB}<\hat{DCB}\)
c: Xét tứ giác ABCD có
AB//CD
AB=CD
Do đó: ABCD là hình bình hành
27 tháng 8
Ta có: \(5x^2+5y^2+8xy-2x+2y+2=0\)
=>\(4x^2+8xy+4y^2+x^2-2x+1+y^2+2y+1=0\)
=>\(4\left(x^2+2xy+y^2\right)+\left(x-1\right)^2+\left(y+1\right)^2=0\)
=>\(4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
=>\(\begin{cases}x+y=0\\ x-1=0\\ y+1=0\end{cases}\Rightarrow\begin{cases}x=1\\ y=-1\end{cases}\)
Khi x=1;y=-1 thì ta có:
\(M=\left(1-1\right)^{2023}+\left(1-2\right)^{2024}+\left(-1+1\right)^{2025}\)
=1
23 tháng 8
a: ta có: EI⊥BF
AC⊥BF
Do đó: EI//AC
=>\(\hat{IEB}=\hat{ACB}\) (hai góc đồng vị)
mà \(\hat{ABC}=\hat{ACB}\) (ΔABC cân tại A)
nên \(\hat{KBE}=\hat{IEB}\)
Xét ΔKBE vuông tại K và ΔIEB vuông tại I có
BE chung
\(\hat{KBE}=\hat{IEB}\)
Do đó: ΔKBE=ΔIEB
=>EK=BI
b: Điểm D ở đâu vậy bạn?
P
1
28 tháng 8
a:
b: TH1: \(\hat{BAD}>90^0;\hat{ABD}>90^0\)
Ta có: ABCD là hình thang
=>\(\hat{ABC}+\hat{BCD}=180^0\)
=>\(\hat{BCD}<180^0-90^0=90^0\)
=>\(\hat{BCD}<\hat{BAD}\)
TH2: \(\hat{ADC}>90^0;\hat{DCB}>90^0\)
Ta có: ABCD là hình thang
DC//AB
=>\(\hat{CDA}+\hat{DAB}=180^0\)
=>\(\hat{DAB}<180^0-90^0=90^0\)
=>\(\hat{DAB}<\hat{DCB}\)
c: Xét tứ giác ABCD có
AB//CD
AB=CD
Do đó: ABCD là hình bình hành
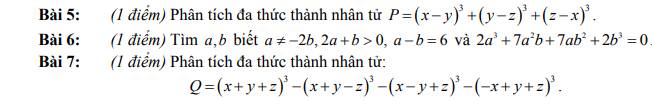
VD5. Đặt a = x - y , b = y - z , c = z - x
=> a + b + c = 0
nên P = (x - y)3 + (y - z)3 + (z - x)3
= a3 + b3 + c3
= (a + b)3 - 3ab(a + b) + c3
= (-c)3 - 3ab(-c) + c3
= 3abc = 3(x - y)(y - z)(z - x)
VD7 : Đặt x + y - z = a ; x - y + z = b ; -x + y + z = c
ta thấy : a + b + c = x + y + z
Nên ta được Q = (x + y + z)3 - (x + y - z)3 - (x - y + z)3 - (-x + y + z)3
= (a + b + c)3 - a3 - b3 - c3
= (a + b)3 + 3(a + b)2c + 3(a + b)c2 + c3 - a3 - b3 - c3
= a3 + b3 + 3ab(a + b) + 3(a + b)c(a + b + c) + c3 - a3 - b3 - c3
= 3(a + b)[ab + c.(a + b + c)]
= 3(a + b)(b + c)(c + a)
= 24xyz