Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trước hết xin nói ngay rằng đồ thị của hàm số y = (2x - 1)(x - 1) là một parabol, không có đường tiệm cận nào cả.
Có lẽ bạn muốn nói đến hàm số y = (2x - 1)/(x - 1).
Nếu đúng vậy thì đồ thị của hàm số là một hyperbol vuông góc có hai đường tiệm cận là đường thẳng x = 1 và đường thẳng y = 2.
Giao điểm của hai đường tiệm cận là I(1; 2).
Gọi M(x,y) là một điểm trên đồ thị. Hệ số góc của đường thẳng IM là
m = (y - 2)/(x - 1) = {[(2x - 1)/(x - 1)] - 2}/(x - 1) = [(2x - 1) - 2(x - 1)]/(x - 1)²
m = 1/(x - 1)²
Hệ số góc của đường tiếp tuyến Mt với đồ thị tại M(x,y) là
m' = dy/dx = -1/(x - 1)²
Muốn cho MI và Mt thẳng góc với nhau thì điều kiện cần và đủ là
mm' = -1
-1/(x - 1)^4 = -1
(x - 1)^4 = 1
(x - 1)² = 1
x - 1 = ±1
x = 0 hay x = 2
Có 2 điểm M thỏa mãn điều kiện của bài toán là (0; 1) và (2; 3)

Trước hết xin nói ngay rằng đồ thị của hàm số y = (2x - 1)(x - 1) là một parabol, không có đường tiệm cận nào cả.
Có lẽ bạn muốn nói đến hàm số y = (2x - 1)/(x - 1).
Nếu đúng vậy thì đồ thị của hàm số là một hyperbol vuông góc có hai đường tiệm cận là đường thẳng x = 1 và đường thẳng y = 2.
Giao điểm của hai đường tiệm cận là I(1; 2).
Gọi M(x,y) là một điểm trên đồ thị. Hệ số góc của đường thẳng IM là
m = (y - 2)/(x - 1) = {[(2x - 1)/(x - 1)] - 2}/(x - 1) = [(2x - 1) - 2(x - 1)]/(x - 1)²
m = 1/(x - 1)²
Hệ số góc của đường tiếp tuyến Mt với đồ thị tại M(x,y) là
m' = dy/dx = -1/(x - 1)²
Muốn cho MI và Mt thẳng góc với nhau thì điều kiện cần và đủ là
mm' = -1
-1/(x - 1)^4 = -1
(x - 1)^4 = 1
(x - 1)² = 1
x - 1 = ±1
x = 0 hay x = 2
Có 2 điểm M thỏa mãn điều kiện của bài toán là (0; 1) và (2; 3)
2, Giao điểm của hai đường tiệm cận là I(1; 2).
Gọi M(x,y) là một điểm trên đồ thị. Hệ số góc của đường thẳng IM là
m = (y - 2)/(x - 1) = {[(2x - 1)/(x - 1)] - 2}/(x - 1) = [(2x - 1) - 2(x - 1)]/(x - 1)²
m = 1/(x - 1)²
Hệ số góc của đường tiếp tuyến Mt với đồ thị tại M(x,y) là
m' = dy/dx = -1/(x - 1)²
Muốn cho MI và Mt thẳng góc với nhau thì điều kiện cần và đủ là
mm' = -1
-1/(x - 1)^4 = -1
(x - 1)^4 = 1
(x - 1)² = 1
x - 1 = ±1
x = 0 hay x = 2
Có 2 điểm M thỏa mãn điều kiện của bài toán là (0; 1) và (2; 3)

b: Thay x=-3 và y=0 vào y=(m-2)x+3, ta được:
-3m+6+3=0
=>m=3

\(a,\Leftrightarrow y=0;x=2\Leftrightarrow2m-2+m-2=0\Leftrightarrow m=\dfrac{4}{3}\)
\(b,\) PT giao Ox: \(\Leftrightarrow\left(m-1\right)x=2-m\Leftrightarrow x=\dfrac{2-m}{m-1}\Leftrightarrow A\left(\dfrac{2-m}{m-1};0\right)\Leftrightarrow OA=\left|\dfrac{2-m}{m-1}\right|\)
PT giao Oy: \(y=m-2\Leftrightarrow B\left(0;m-2\right)\Leftrightarrow OB=\left|m-2\right|\)
\(S_{OAB}=\dfrac{2}{3}\Leftrightarrow\dfrac{1}{2}OA\cdot OB=\dfrac{2}{3}\Leftrightarrow\left|\dfrac{2-m}{m-1}\cdot\left(m-2\right)\right|=\dfrac{4}{3}\\ \Leftrightarrow\left|\dfrac{-\left(m-2\right)^2}{m-1}\right|=\dfrac{4}{3}\Leftrightarrow\left[{}\begin{matrix}\dfrac{-\left(m-2\right)^2}{m-1}=\dfrac{4}{3}\left(1\right)\\\dfrac{-\left(m-2\right)^2}{1-m}=\dfrac{4}{3}\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow-3m^2+12m-12=4m-4\\ \Leftrightarrow3m^2-9m+9=0\\ \Leftrightarrow m\in\varnothing\\ \left(2\right)\Leftrightarrow-3m^2+12m-12=4-4m\\ \Leftrightarrow3m^2-16m+16=0\\ \Leftrightarrow\left[{}\begin{matrix}m=4\\m=\dfrac{4}{3}\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}m=4\\m=\dfrac{4}{3}\end{matrix}\right.\) thỏa đề
\(c,\) Gọi \(E\left(x_0;y_0\right)\) là điểm cần tìm
\(\Leftrightarrow\left(m-1\right)x_0+m-2=y_0\\ \Leftrightarrow mx_0+m-x_0-y_0-2=0\\ \Leftrightarrow m\left(x_o+1\right)-\left(x_0+y_0+2\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0=-1\\y_0=-2-x_0=-1\end{matrix}\right.\Leftrightarrow E\left(-1;-1\right)\)

a: Phương trình hoành độ giao điểm là:
2x=-3x+5
=>5x=5
=>x=1
Thay x=1 vào y=2x, ta được:
\(y=2\cdot1=2\)
Vậy: M(1;2)
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\-3x+5=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\x=\dfrac{5}{3}\end{matrix}\right.\)
Vậy: A(5/3;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=-3\cdot0+5=5\end{matrix}\right.\)
Vậy: B(0;5)
O(0;0); A(5/3;0); B(0;5)
=>\(OA=\sqrt{\left(\dfrac{5}{3}-0\right)^2+\left(0-0\right)^2}=\dfrac{5}{3}\)
\(OB=\sqrt{\left(0-0\right)^2+\left(5-0\right)^2}=5\)
Vì A,B là giao điểm của (d): y=-3x+5 với trục Ox và trục Oy nên ΔOAB vuông tại O
=>\(S_{AOB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot\dfrac{5}{3}\cdot5=\dfrac{25}{6}\)
M(1;2); O(0;0); A(5/3;0)
\(OA=\sqrt{\left(\dfrac{5}{3}-0\right)^2+\left(0-0\right)^2}=\dfrac{5}{3}\)
\(OM=\sqrt{\left(1-0\right)^2+\left(2-0\right)^2}=\sqrt{5}\)
\(MA=\sqrt{\left(\dfrac{5}{3}-1\right)^2+\left(0-2\right)^2}=\dfrac{2\sqrt{10}}{3}\)
Xét ΔOAM có \(cosAOM=\dfrac{OA^2+OM^2-AM^2}{2\cdot OA\cdot OM}=\dfrac{\sqrt{5}}{5}\)
=>\(sinAOM=\sqrt{1-\left(\dfrac{\sqrt{5}}{5}\right)^2}=\dfrac{2}{\sqrt{5}}\)
\(S_{AOM}=\dfrac{1}{2}\cdot OA\cdot OM\cdot sinAOM\)
\(=\dfrac{1}{2}\cdot\sqrt{5}\cdot\dfrac{5}{3}\cdot\dfrac{2}{\sqrt{5}}=\dfrac{5}{3}\)

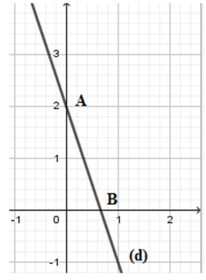
B (x; 0) là giao điểm của d với trục hoành nên 0 = − 3 x + 2 ⇔ x = 2 3 B 2 3 ; 0
A (0; y) là giao điểm của d với trục tung nên y = − 3 . 0 + 2 ⇔ y = 2 ⇒ A ( 0 ; 2 )
Suy ra O A = | 2 | = 2 ; O B = 2 3 = 2 3
Vì tam giác OAB vuông tại O nên SOAB = O A . O B 2 = 2. 2 3 2 = 2 3 (đvdt)
Đáp án cần chọn là: D
Do A là giao (d) với trục tung \(\Rightarrow x_A=0\Rightarrow y_A=\left(m-2\right).0+m-1=m-1\)
\(\Rightarrow OA=\left|y_A\right|=\left|m-1\right|\)
Do B là giao (d) với trục hoành
\(\Rightarrow y_B=0\Rightarrow\left(m-2\right)x_B+m-1=0\Rightarrow x_B=-\dfrac{m-1}{m-2}\) (với \(m\ne2\))
\(\Rightarrow OB=\left|x_B\right|=\left|\dfrac{m-1}{m-2}\right|\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{1}{2}.\left|m-1\right|.\left|\dfrac{m-1}{m-2}\right|=1\)
\(\Rightarrow\left(m-1\right)^2=2\left|m-2\right|\) (1)
TH1: \(m>2\)
(1) \(\Leftrightarrow m^2-2m+1=2m-4\Rightarrow m^2-4m+5=0\) (vô nghiệm)
TH2: \(m< 2\)
\(\left(1\right)\Leftrightarrow m^2-2m+1=2\left(2-m\right)\Leftrightarrow m^2+2m-3=0\)
\(\Rightarrow\left\{{}\begin{matrix}m=1\\m=-3\end{matrix}\right.\) (thỏa mãn)
TH2: `m^2 -2m+1=2(2-m)`
`<=>m^2 -2m+1=4-2m`
`<=>m^2 -2m+1-4+2m=0`
`<=>m^2-3=0` mà thầy??