Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hết luôn đó bạn Ngọc Vi ... nhưng bạn giúp được câu nào thì mình cảm ơn

Ta có \(m=1-x^2\le1\) . Vậy ta xét các khoảng giá trị của m :
+ Nếu m = 1 thì \(x=0\) thỏa mãn nghiệm duy nhất.
+ Nếu \(0\le m< 1\) thì \(1-m>0\) , vậy lúc đó pt có hai nghiệm
\(x=\pm\sqrt{1-m}\)
+ Nếu \(m=0\) thì \(x=\pm1\)
+ Nếu \(m< 0\) thì \(x^2=1+m\Leftrightarrow x=\pm\sqrt{1+m}\) luôn có hai nghiệm.
Vậy m = 1 thỏa mãn đề bài.

Bài 6
Để phương trình có vô số nghiệm thì
m+n-3=0 và 2m-3n+4=0
=>m+n=3 và 2m-3n=-4
=>m=1; n=2

a/ \(f\left(x\right)\ge2\sqrt{\frac{16x^2}{x^2}}=8\)
Dấu "=" xảy ra khi \(x^2=\frac{16}{x^2}\Leftrightarrow x=\pm2\)
b/ Hàm này không tồn tại GTNN
c/ \(f\left(x\right)=x+3+\frac{25}{x+3}-4\ge2\sqrt{\frac{25\left(x+3\right)}{x+3}}-4=6\)
Dấu "=" xảy ra khi \(x+3=\frac{25}{x+3}\Leftrightarrow x=2\)
d/ \(f\left(x\right)=x+\frac{9}{x}+3\ge2\sqrt{\frac{9x}{x}}+3=9\)
Dấu "=" xảy ra khi \(x=\frac{9}{x}\Leftrightarrow x=3\)
Chọn A
Ta có –x2+x-1= 0 vô nghiệm,
6x2- 5x+1= 0 khi x= ½ hoặc x= 1/3
Bảng xét dấu
Suy ra f(x) > 0 khi và chỉ khi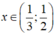
Và f( x)< 0 khi và chỉ khi