Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta biết hàm số y = f(x) có cực trị khi phương trình y’ = 0 có nghiệm và y’ đổi dấu khi qua các nghiệm đó.
Ta có:
Xét y’ = 0, ta có: y′ = 3 x 2 − 2mx + (m – 2/3)
∆ ’ > 0 khi m < 1 hoặc m > 2 (∗)
Để hàm số có cực trị tại x = 1 thì
y′(1) = 3 − 2m + m – 2/3 = 0 ⇔ m = 7/3, thỏa mãn điều kiện (∗)
Với m = 7/3 thì hàm số đã cho trở thành:
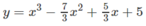
Ta có:
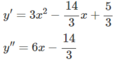
Vì y′′(1) = 6 – (14/3) > 0 nên hàm số đạt cực tiểu tại x = 1 và y CT = y(1) = (16/3).

Ta biết hàm số y = f(x) có cực trị khi phương trình y’ = 0 có nghiệm và y’ đổi dấu khi qua các nghiệm đó.
Ta có:
Xét y’ = 0, ta có: y′ = 3 x 2 − 2mx + (m – 2/3)
Δ’ > 0 khi m < 1 hoặc m > 2 (∗)
Để hàm số có cực trị tại x = 1 thì
y′(1) = 3 − 2m + m – 2/3 = 0 ⇔ m = 7/3, thỏa mãn điều kiện (∗)
Với m = 7/3 thì hàm số đã cho trở thành:
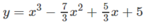
Ta có:
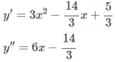
Vì y′′(1) = 6 – (14/3) > 0 nên hàm số đạt cực tiểu tại x = 1 và y C T = y(1) = (16/3).

Tập xác định :
Nếu hàm số đạt cực đại tại x = 2 thì y'(2) = 0 ⇔ m2 + 4m + 3 = 0 ⇔ m=-1 hoặc m=-3
- Với m = -1, ta có :
x=0 hoặc x=2.
Ta có bảng biến thiên :
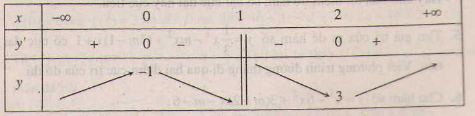
Trường hợp này ta thấy hàm số không đạt cực đại tại x = 2.
- Với m = -3, ta có:
x=2 hoặc x=4
Ta có bản biến thiên :
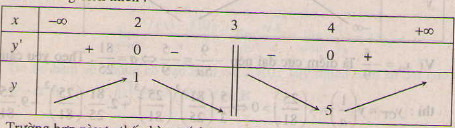
Trường hợp này ta thấy hàm số đạt cực đại tại x = 2.
Vậy m = -3 là giá trị cần tìm.

- Khi \(m=0\Rightarrow y=x-1\) nên hàm số không có cực trị
- Khi \(m\ne0\Rightarrow y'=3mx^2+6mx-\left(m-1\right)\)
hàm số không có cực trị khi và chỉ chỉ y' = 0 không có nghiệm hoặc có nghiệm kép
\(\Leftrightarrow\Delta'=9m^2+3m\left(m-1\right)=12m^2-3m\le0\) \(\Leftrightarrow0\le m\)\(\le\frac{1}{4}\)

Ta có \(y'=3x^2-6\left(m+1\right)x+9\)
Hàm số đạt cực đại, cực tiểu tại \(x_1,x_2\) \(\Leftrightarrow\) phương trình \(y'=0\) có hai nghiệm phân biệt là \(x_1,x_2\)

\(y'=3x^2-4x+m\)
Để hàm số đạt cực tiểu tai x = 1 thì x = 1 là nghiệm của y' và y' đổi dấu khi đi qua x = 1.
Để x = 1 là nghiệm của y' thì:
\(3.1^2-4.1+m=0\) \(\Rightarrow m=1\)
Với m = 1. khi đó: \(y'=3x^2-4x+1\) có 2 nghiệm là \(1\) và \(\dfrac{1}{3}\); \(y'\) đổi dấu từ âm sang dương khi đi qua x = 1. Vậy hàm số có cực tiểu tại x = 1.

\(\Leftrightarrow y'=0\)
có 2 nghiệm phân biệt \(x_1,x_2\) thỏa mãn \(x_1\)<\(x_2\)<1
\(\Leftrightarrow\)\(\begin{cases}\Delta'=4m^2-m-5>0\\f\left(1\right)=-5m+7>0\\\frac{S}{2}=\frac{2m-1}{3}<1\end{cases}\)\(\Leftrightarrow\)\(\frac{5}{4}\)<m<\(\frac{7}{5}\)



\(y'=3x^2-2mx+\left(m-\dfrac{2}{3}\right)\)
Để hàm số có cực trị tại x = 1 thì x =1 phải là nghiệm của y'=0.
=> \(3.1^2-2m.1+\left(m-\dfrac{2}{3}\right)=0\)
\(\Leftrightarrow m=\dfrac{7}{3}\)
Khi đó ta có:
\(y=x^3-\dfrac{7}{3}x^2+\dfrac{5}{3}x+5\)
\(y'=3x^2-2mx+\left(m-\dfrac{2}{3}\right)=\dfrac{1}{3}\left(9x^2-14x+5\right)\)
\(y'\) có 2 nghiệm là \(1\) và \(\dfrac{5}{9}\).
\(y'\) đổi dấu từ âm sang dương khi đi qua x = 1 nên tại x = 1 thì hàm số đạt cực tiểu.
Giá trị cực tiểu tại x = 1 là:
\(y\left(1\right)=1^3-\dfrac{7}{3}.1^2+\dfrac{5}{3}.1+5=\dfrac{16}{3}\)