PH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
24 tháng 1 2017
Chọn B
Ta có: 
. Gọi 
suy ra 
, ta có 
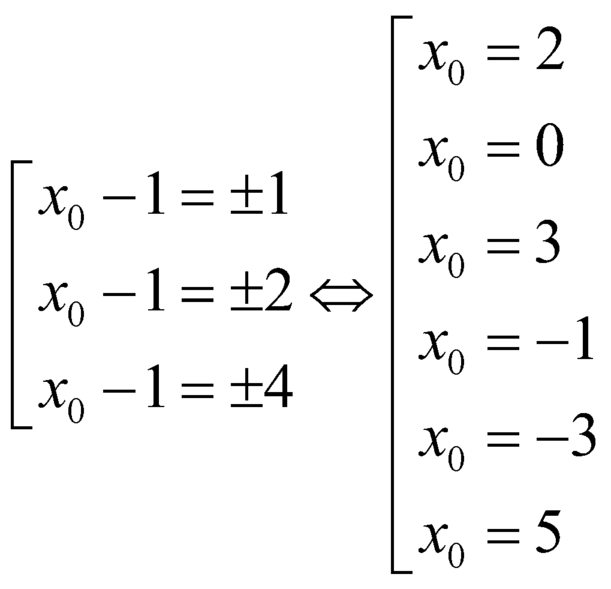. Vậy có 
điểm có tọa độ nguyên.
CM
15 tháng 2 2017
Đáp án B
Từ giả thiết
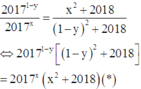
Xét hàm số
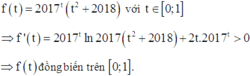
Do đó (*)
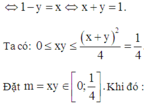
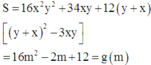
Xét hàm g(m) trên đoạn
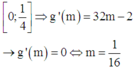
Lúc này
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 6 2019
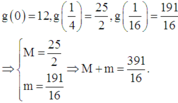
\(log_{\frac{1}{2}}x+log_{\frac{1}{2}}y\le log_{\frac{1}{2}}\left(x+y^2\right)\Leftrightarrow log_{\frac{1}{2}}\left(xy\right)\le log_{\frac{1}{2}}\left(x+y^2\right)\Leftrightarrow xy\ge x+y^2\)
\(\Leftrightarrow x\left(y-1\right)\ge y^2\Leftrightarrow\left\{{}\begin{matrix}y>1\\x\ge\frac{y^2}{y-1}\end{matrix}\right.\)
\(\Rightarrow P=x+3y\ge\frac{y^2}{y-1}+3y=4y+1+\frac{1}{y-1}=4\left(y-1\right)+\frac{1}{y-1}+5\)
\(\Rightarrow P\ge2\sqrt{4\left(y-1\right).\frac{1}{\left(y-1\right)}}+5=9\)
\(\Rightarrow P_{min}=9\) khi \(\left\{{}\begin{matrix}x=\frac{9}{2}\\y=\frac{3}{2}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 6 2021
Xét hàm \(f\left(x\right)=x^5-5x^3-20x+m\)
\(f'\left(x\right)=5x^4-15x^2-20=0\) có 2 nghiệm
\(\Rightarrow f\left(x\right)\) có 2 cực trị
\(\Rightarrow y=\left|f\left(x\right)\right|\) có 5 cực trị khi \(x^5-5x^3-20x+m=0\) có 3 nghiệm bội lẻ
Từ BBT ta thấy \(y=-m\) cắt \(y=x^5-5x^3-20x\) tại 3 điểm pb khi và chỉ khi:
\(-48\le-m\le48\Rightarrow-48\le m\le48\)
\(\Rightarrow\) Có 97 giá trị nguyên của m
CM
8 tháng 5 2018
Đáp án C
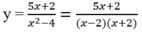
Đồ thị có hai tiệm cận đứng là x = 2 và x = -2 và có một tiệm cận ngang là y = 0
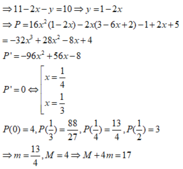
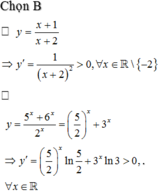
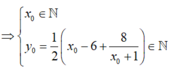
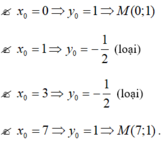
\(x=3y\) và y = 5\(x\) thay y = 5\(x\) vào \(x\) = 3y ta có: \(x\) = 3.5\(x\)
⇒ \(x\) = 15\(x\) ⇒ \(x-15x\) = 0 ⇒ \(-14\)\(x\) = 0 ⇒ \(x=0\)
Thay \(x\) = 0 vào y = 5\(x\) ta được: y= 5.0 = 0
Vậy \(x=3\)y; y = 5\(x\) thì y = 0