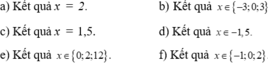K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 3 2021
a) Ta có: \(x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Leftrightarrow x-1=0\)hay x=1
Vậy: S={1}
c) Ta có: \(x+x^4=0\)
\(\Leftrightarrow x\left(x^3+1\right)=0\)
\(\Leftrightarrow x\left(x+1\right)\left(x^2-x+1\right)=0\)
mà \(x^2-x+1>0\forall x\)
nên x(x+1)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
Vậy: S={0;-1}
VM
25 tháng 10 2019
\(2x^2-6x=0\)
\(\Rightarrow2x.\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2x=0\\x-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0:2\\x=0+3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
Vậy \(x\in\left\{0;3\right\}.\)
\(2x.\left(x+2\right)-3.\left(x+2\right)=0\)
\(\Rightarrow\left(x+2\right).\left(2x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+2=0\\2x-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0-2\\2x=3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-2\\x=3:2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-2\\x=\frac{3}{2}\end{matrix}\right.\)
Vậy \(x\in\left\{-2;\frac{3}{2}\right\}.\)
\(x^3-16x=0\)
\(\Rightarrow x.\left(x^2-16\right)=0\)
\(\Rightarrow x.\left(x^2-4^2\right)=0\)
\(\Rightarrow x.\left(x-4\right).\left(x+4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x-4=0\\x+4=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=0+4\\x=0-4\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)
Vậy \(x\in\left\{0;4;-4\right\}.\)
Chúc bạn học tốt!
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
18 tháng 7 2023
a, (\(x-2\))2 - (2\(x\) + 3)2 = 0
(\(x\) - 2 - 2\(x\) - 3)(\(x\) - 2 + 2\(x\) + 3) = 0
(-\(x\) - 5)(3\(x\) +1) = 0
\(\left[{}\begin{matrix}-x-5=0\\3x+1=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-5\\3x=-1\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-5\\x=-\dfrac{1}{3}\end{matrix}\right.\)
Vậy \(x\in\) { -5;- \(\dfrac{1}{3}\)}
b, 9.(2\(x\) + 1)2 - 4.(\(x\) + 1)2 = 0
{3.(2\(x\) + 1) - 2.(\(x\) +1)}{ 3.(2\(x\) +1) + 2.(\(x\) +1)} = 0
(6\(x\) + 3 - 2\(x\) - 2)(6\(x\) + 3 + 2\(x\) + 2) = 0
(4\(x\) + 1)(8\(x\) + 5) =0
\(\left[{}\begin{matrix}4x+1=0\\8x+5=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-\dfrac{1}{4}\\x=-\dfrac{5}{8}\end{matrix}\right.\)
S = { - \(\dfrac{5}{8}\); \(\dfrac{-1}{4}\)}
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
18 tháng 7 2023
d, \(x^2\)(\(x\) + 1) - \(x\) (\(x+1\)) + \(x\)(\(x\) -1) = 0
\(x\left(x+1\right)\).(\(x\) - 1) + \(x\)(\(x\) -1) = 0
\(x\)(\(x\) -1)(\(x\) + 1 + 1) = 0
\(x\left(x-1\right)\left(x+2\right)\) = 0
\(\left[{}\begin{matrix}x=0\\x-1=0\\x+2=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=1\\x=-2\end{matrix}\right.\)
S = { -2; 0; 1}
MA
3
30 tháng 9 2016
\(x^2-25+2\left(x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(x-5\right)+2\left(x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(x-5+2\right)=0\)
\(\left(x+5\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+5=0\\x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-5\\x=3\end{cases}}}\)
20 tháng 1 2018
\(x\left(x-1\right)+x-1=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\x+1=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=1\\x=-1\end{cases}}\)
P/s tham khảo nha
TP
12 tháng 7 2019
a)\(x^2-3x=0\)
\(\Leftrightarrow x\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
b)2x ( x - 2 ) - (x - 2 ) = 0
\(\Leftrightarrow\left(x-2\right)\left(2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\2x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\frac{1}{2}\end{matrix}\right.\)
c)\(x+5x^2=0\)
\(\Leftrightarrow x\left(1+5x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\1+5x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\frac{1}{5}\end{matrix}\right.\)
TP
12 tháng 7 2019
\(x^3+x=0\)
\(\Leftrightarrow x\left(x^2+1\right)=0\)
Vì \(x^2+1>0\forall x\)
nên x=0
21 tháng 7 2020
a) ( x - 3 )2 - 4 = 0
<=> ( x - 3 )2 = 4
<=> \(\orbr{\begin{cases}\left(x-3\right)^2=2^2\\\left(x-3\right)^2=\left(-2\right)\end{cases}}\)
<=> \(\orbr{\begin{cases}x-3=2\\x-3=-2\end{cases}}\)
<=> \(\orbr{\begin{cases}x=5\\x=1\end{cases}}\)
Vậy S = { 5 ; 1 }
b) x2 - 9 = 0
<=> x2 = 9
<=> \(\orbr{\begin{cases}x^2=3^2\\x^2=\left(-3\right)^2\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\\x=-3\end{cases}}\)
Vậy S = { 3 ; -3 }
c) x( x - 2x ) - x2 - 8 = 0
<=> x2 - 2x2 - x2 - 8 = 0
<=> -2x2 - 8 = 0
<=> -2x2 = 8
<=> x2 = -4 ( vô lí )
<=> x = \(\varnothing\)
Vậy S = { \(\varnothing\)}
21 tháng 7 2020
d) 2x( x - 1 ) - 2x2 + x - 5 = 0
<=> 2x2 - 2x - 2x2 + x - 5 = 0
<=> -x - 5 = 0
<=> -x = 5
<=> x = -5
Vậy S = { -5 }
e) x( x - 3 ) - ( x + 1 )( x - 2 ) = 0
<=> x2 - 3x - ( x2 - x - 2 ) = 0
<=> x2 - 3x - x2 + x + 2 = 0
<=> - 2x + 2 = 0
<=> -2x = -2
<=> x = 1
Vậy S = { 1 }
f) x( 3x - 1 ) - 3x2 - 7x = 0
<=> 3x2 - x - 3x2 - 7x = 0
<=> -8x = 0
<=> x = 0
Vậy S = { 0 }
TL
1
NH
13 tháng 2 2023
a)
`x^2 +5x+6=0`
`<=> x^2 + 3x +2x+6=0`
`<=> x(x+3)+2(x+3)=0`
`<=> (x+3)(x+2)=0`
`<=> x+3=0 hoặcx+2=0`
`<=> x=-3 hoặc x=-2`
b)
`x^2 -7x+6=0`
`<=> x^2 -6x-x+6=0`
`<=> x(x-6)-(x-6)=0`
`<=> (x-6)(x-1)=0`
`<=> x-6=0 hoặc x-1=0 `
`<=> x=6 hoặc x=1`
c)
`x^2 +x -12=0`
`<=> x^2 +4x-3x-12=0`
`<=> x(x+4)-3(x+4)=0`
`<=> (x+4)(x-3)=0`
`<=> x+4=0 hoặc x-3=0`
`<=> x=-4 hoặc x=3`
d)
`x^2 -x-6=0`
`<=>x^2 -3x+2x-6=0`
`<=> x(x-3)+2(x-3)=0`
`<=> (x-3)(x+2)=0`
`<=> x-3=0 hoặc x+2=0`
`<=> x=3 hoặc x=-2`
e)
`2x^2 -3x-5=0`
`<=> 2x^2 -5x+2x-5=0`
`<=> x(2x-5)+(2x-5)=0`
`<=> (2x-5)(x+1)=0`
`<=> 2x-5=0 hoặc x+1=0`
`<=> x=5/2 hoặc x=-1`