Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. b.
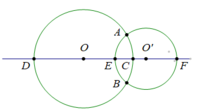
c. - Đường tròn (O’; 1cm) có đường kính là: EF; Các dây cung là: EA, EB, AB, FA, FB
Vì E thuộc (O’; 1cm) nên EO’=1cm; EF=2.EO’=2cm
- Đường tròn (O; 1,5cm) có đường kính là: DC; Các dây cung là: DA, DB, AB, AC, CB
Vì C thuộc (O; 1,5cm) nên CO=1,5cm; DC=2.CO=3cm
d. Vì đường tròn (O’; 1cm) cắt đoạn thẳng OO’ tại E, nên E nằm giữa 2 điểm O và O’.
Ta có: O E + E O ' = O O ' ⇒ O E = 1 c m
Mà EO’=1cm, nên OE=EO’ (=1cm)
Do đó: E là trung điểm của đợn thẳng OO’.
e. Vì đường tròn (O; 1cm) cắt đường thẳng OO’ tại D, đường tròn (O’; 1cm) cắt đường thẳng OO’ tại F, nên 4 điểm D, O, O’, F lần lượt theo thứ tự đó và DO=1,5cm; O’F=1cm.
Ta có: D F = D O + O O ' + O ' F = 1 , 5 + 2 + 1 = 4 , 5 c m .
Vậy DF=4,5cm

a) Lấy 1 điểm trong 50 điểm, từ điểm đó nối với các điểm còn lại ta được 49 đường thẳng
Làm tương tự với các điểm còn lại ta được \(49.50=2450\)đường thẳng
mà mỗi đường thẳng trùng nhau 2 lần nên số đường thẳng thực có là: \(\frac{2450}{2}=1225\)đường thẳng
a )
Cứ 1 điểm lại có thể tạo với 49 điểm còn lại tạo thành 49 đường thẳng
=> Có : 49 . 100 = 4900 ( đường thẳng )
Thực chất số đường thẳng này đã được tính 2 lần
=> Số đường thẳng thực là :
4900 : 2 = 2450 ( đường thẳng )