

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




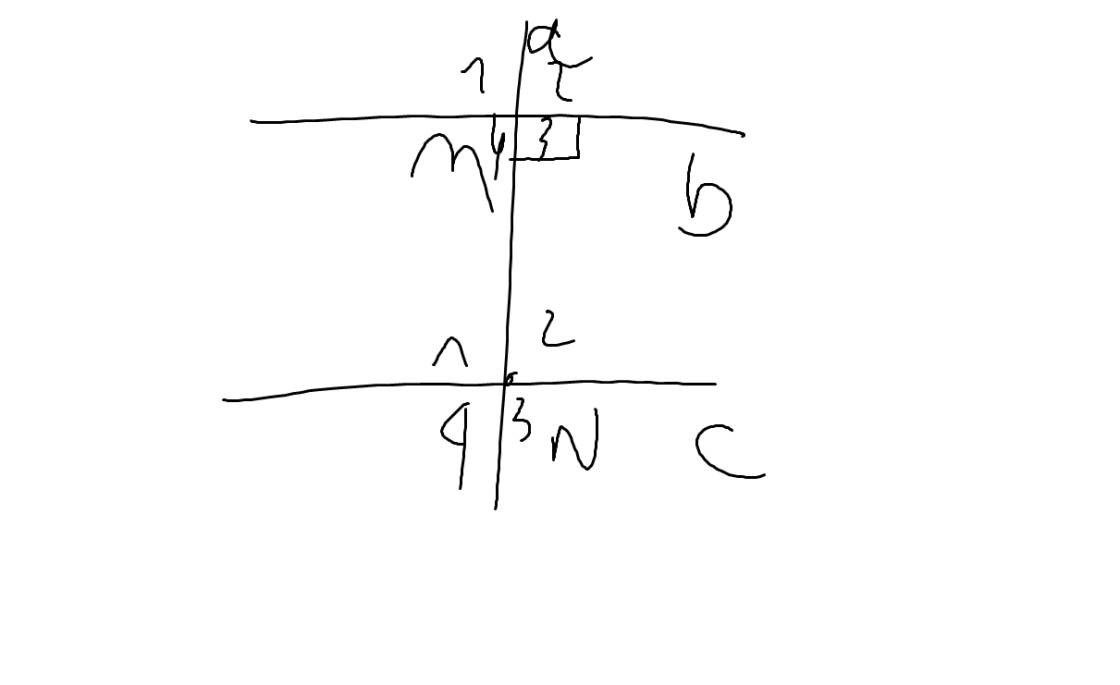
| GT | a\(\perp\)b tại M a cắt c tại N b//c |
| KL | a\(\perp\)c tại N |
Chứng minh định lí:
Ta có: b//c
=>\(\widehat{M_3}=\widehat{N_1}\)(hai góc so le trong)
mà \(\widehat{M_3}=90^0\)
nên \(\widehat{N_1}=90^0\)
=>a\(\perp\)c tại N

d:
Giả thiết: \(\widehat{xAy}\) và \(\widehat{x'Ay'}\) là hai góc đối đỉnh
Kết luận: \(\widehat{xAy}=\widehat{x'Ay'}\)


Giả sử cho 2 đường thẳng song song a và b, đường thẳng c vuông góc với a. Ta phải chứng minh c cũng vuông góc với b.
Thật vậy,
Vì a//b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) ( 2 góc đồng vị), mà \(\widehat {{A_1}} = 90^\circ \)nên \(\widehat {{B_1}} = 90^\circ \) hay \(b \bot c\)(đpcm)

a)
| GT |
a \(\perp\) c b \(\perp\) c |
| KL | a // b |
b)
| GT |
a // c b // c |
| KL | a // b |

Hình trên biểu thị đường thẳng x' cắt 2 đườg thẳng x và y tạo nên các cặp góc so le trong, ngoài, đồng vị bằng nhau
Kí hiệu :
GT đường thẳng a và d cùng vuông góc vs 1 đường thẳng
KL a và b song song