
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Hình trên biểu thị đường thẳng x' cắt 2 đườg thẳng x và y tạo nên các cặp góc so le trong, ngoài, đồng vị bằng nhau
Kí hiệu :
GT đường thẳng a và d cùng vuông góc vs 1 đường thẳng
KL a và b song song

a:
| GT | góc AOB và góc COD là hai góc đối đỉnh |
| KL | góc AOB=góc COD |
b:
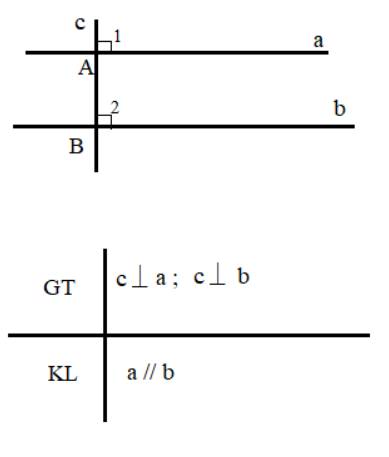
| GT | a\(\perp\)b, c\(\perp\)b |
| KL | a//c |

GT:Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba
KL:Chúng song song với nhau.
Giả thiết: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba
Kết luận: chúng song song với nhau

a)
| GT |
a \(\perp\) c b \(\perp\) c |
| KL | a // b |
b)
| GT |
a // c b // c |
| KL | a // b |

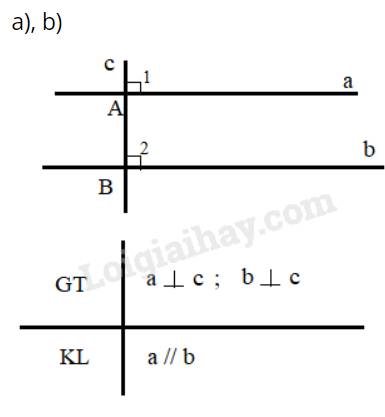
c) Giả sử có 2 đường thẳng phân biệt a,b cùng vuông góc với một đường thẳng c.
Ta có: \(\widehat {{A_1}} = \widehat {{B_2}}\), mà hai góc này ở vị trí đồng vị nên a//b (Dấu hiệu nhận biết 2 đường thẳng song song)
Như vậy, định lí trên có thể được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song.