K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

13 tháng 6 2023
a: góc ONM+góc OPM=180 độ
=>ONMP nội tiếp
b: góc OHM=góc ONM=90 độ
=>OHNM nội tiếp
=>góc MON=góc MHN

19 tháng 4 2017
Lười quá, chắc mình giải câu c thôi ha.
Vẽ \(OH\) vuông góc \(d\) tại \(H\). \(AB\) cắt \(OH\) tại \(L\). \(OM\) cắt \(AB\) tại \(T\)
H M A B O d L T .
CM được \(OL.OH=OT.OM=R^2\) nên \(L\) cố định. Vậy \(AB\) luôn qua \(L\) cố định.
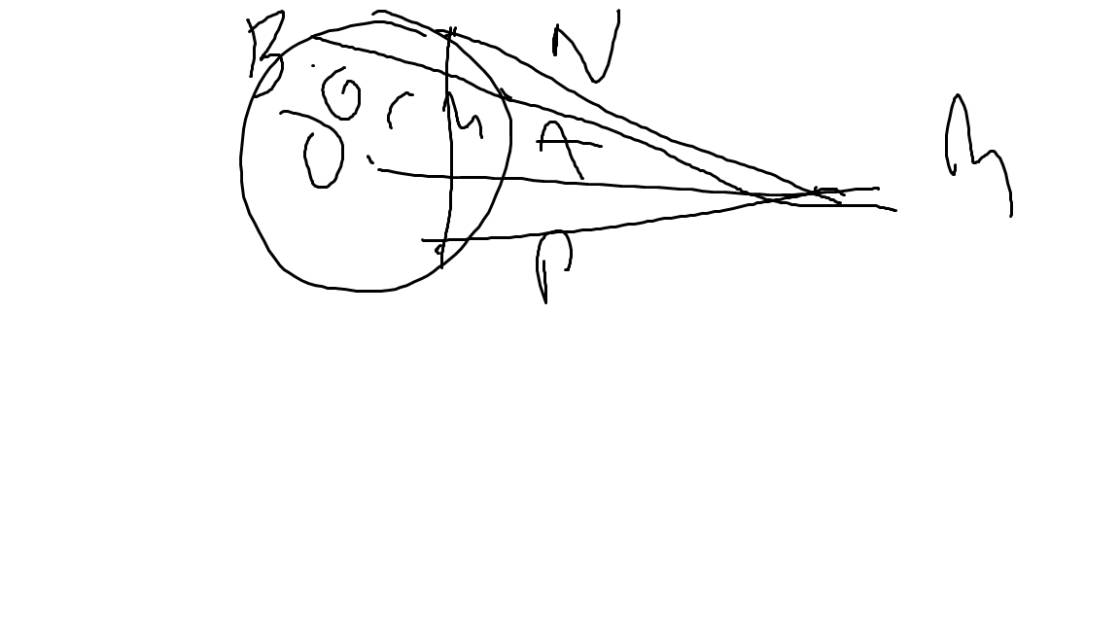
a: Xét tứ giác OPMN có \(\widehat{OPM}+\widehat{ONM}=180^0\)
nên OPMN là tứ giác nội tiếp
b: \(MN=\sqrt{10^2-6^2}=8\left(cm\right)\)
a. MN là tiếp tuyến của (O ; 6cm) \(\Rightarrow MN\perp ON\left(a\right)\)
MP là tiếp tuyến của (O ; 6cm) \(\Rightarrow MP\perp OP\left(b\right)\)
Từ (a), (b), vậy : OPMN là tứ giác nội tiếp.
b. Do \(MN\perp ON\) ⇒ △MNO vuông tại N.
Áp dụng định lí Py-ta-go :
\(MO^2=MN^2+ON^2\)
\(\Leftrightarrow MN=\sqrt{MO^2-ON^2}=\sqrt{10^2-6^2}=8\left(cm\right)\)
c. H là trung điểm AB ⇒ \(OH\perp AB\left(c\right)\)
Từ (a), (c) ⇒ Tứ giác MNOH nội tiếp được một đường tròn.
Vậy : \(\hat{MHN}=\hat{MON}\) (cùng chắn cung MN).
d. Gọi diện tích của hình viên phân là S.
\(S=S_{OAB}-S_{\Delta AOB}\left(d\right)\)
Ta có : \(OA=OB=AB=6\left(cm\right)\)
⇒ △OAB là tam giác đều.
\(\Rightarrow S_{\Delta AOB}=9\sqrt{3}\left(cm^2\right)\)
Lại có : \(S_{AOB}=\dfrac{\text{π}R^2n}{360}=\dfrac{\text{π}.6^2.60}{360}=6\text{π}\left(cm^2\right)\)
Thay lại vào (d) : \(S=6\text{π}-9\sqrt{3}\approx3,26\left(cm^2\right)\)