Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(23,3\) phút; \(540^0;27,6^0C\)
b) Khi lấy số trung bình làm đại diện cho các số liệu thống kê về quy mô và độ lớn, có thể xem rằng mỗi ngày bạn A đi từ nhà đến trường đều mất 23,3 phút.
Tương tự, nêu ý nghĩa số trung bình của các số liệu thống kê cho ở bảng 7 và bảng 8.

B A C H
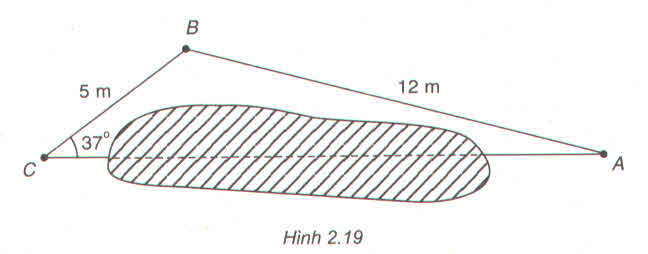
Hạ \(BH\perp AC\).
\(CH=CB.sin37^o\approx3m.\)
Áp dụng định lý Pi-ta-go trong tam giác vuông BCH:
\(BH=\sqrt{AB^2-AH^2}=\sqrt{5^2-3^2}=4m\).
Áp dụng định lý Pi-ta-go trong tam giác vuông BHA:
\(HA=\sqrt{BC^2-BH^2}=\sqrt{12^2-4^2}=8\sqrt{2}m\).
\(AC=AH+HC=8\sqrt{2}+3m\).

A B C A' B' C' H
Tọa độ điểm A là giao điểm của AB và AA'
\(\left\{{}\begin{matrix}4x+y-12=0\\2x+2y-9=0\end{matrix}\right.\)<=>\(\left\{{}\begin{matrix}x=2,5\\y=2\end{matrix}\right.\)
=>A(2,5;2)
Tọa độ điểm B là giao điểm của AB và BB'
\(\left\{{}\begin{matrix}4x+y-12=0\\5x-4y-15=0\end{matrix}\right.\)<=>\(\left\{{}\begin{matrix}x=3\\y=0\end{matrix}\right.\)
=>B(3;0)
AA' vuông góc với BC
=>VTCP của BC là VTPT của AA': \(\overrightarrow{n}=\left(1;1\right)\)
=>VTPT của BC là: \(\overrightarrow{n'}=\left(1;-1\right)\)và B(3;0) thuộc BC
Phương trình đường thẳng BC: 1(x-3)-1(y-0)=0
hay (BC): x-y-3=0
BB' vuông góc với AC
=>VTCP của AC là: \(\overrightarrow{m}=\left(5;-4\right)\)
=>VTPT của AC là: \(\overrightarrow{m'}=\left(4;5\right)\) và A(2,5;2) thuộc AC
=>(AC): 4(x-2,5)+5(y-2)=0
hay (AC):4x+5y-20=0
Vậy...

\(a,AC=\sqrt{\left(4-7\right)^2+\left(6-\dfrac{3}{2}\right)^2}=\sqrt{9+\dfrac{81}{4}}=\dfrac{3\sqrt{13}}{2}\\ AB=\sqrt{\left(4-1\right)^2+\left(6-4\right)^2}=\sqrt{9+4}=\sqrt{13}\\ BC=\sqrt{\left(1-7\right)^2+\left(4-\dfrac{3}{2}\right)^2}=\sqrt{36+\dfrac{25}{4}}=\dfrac{13}{2}\)


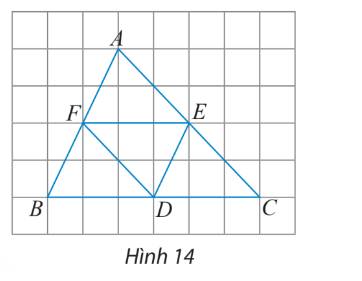
Từ giả thiết ta có:
\(AF = FB = ED\); \(AE = EC = FD\); \(BD = DC = EF\)
Từ đó dựa vào hình ta có:
a) Các vectơ bằng vectơ \(\overrightarrow {EF} \)là \(\overrightarrow {DB} \) và \(\overrightarrow {CD} \)
b) Các vectơ đối vectơ \(\overrightarrow {EC} \) là \(\overrightarrow {EA} \) và \(\overrightarrow {DF} \)