Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

có cần phải tốn tiền v k pạn?quyền lợi của bn mà. trách nhiệm của quản lí và thầy cô là bảo vệ nk của bn

Theo bài ra :
\(\left(x+5\right)\left(x^2-1\right)\left(3-x\right)>0\)
<=> \(\left(x+5\right)\left(x-1\right)\left(x+1\right)\left(3-x\right)>0\)
Đặt \(\left(x+5\right)\left(x-1\right)\left(x+1\right)\left(3-x\right)=A\)
Ta có bảng xét dấu :
| \(-\infty\) | -5 | -1 | 1 | 3 | \(+\infty\) | ||||
| (x+5) | - | 0 | + | + | + | + | |||
| x2-1 | + | + | 0 | - | 0 | + | + | ||
| 3-x | + | + | + | + | 0 | - | |||
| A | - (loại) | 0 (loại) | +(t.m) | 0(loại) | -(loại) | 0(loại) | +(t.m) | 0(loại) | -(loại) |
Từ bảng xét dấu trên suy ra :
\(A>0\Rightarrow\left[{}\begin{matrix}-5< x< -1\\1< x< 3\end{matrix}\right.\)

\(2x-49=5.3^2\)
\(\Rightarrow2x-49=5.9\)
\(\Rightarrow2x=45+49\)
\(\Rightarrow2x=94\)
\(\Rightarrow x=94:2\)
\(\Rightarrow x=47\)

Trực tâm H là giao điểm của BH và AH ⇒ tọa độ H là nghiệm của hệ:
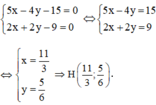
A là giao điểm của AB và AH nên tọa độ A là nghiệm của hệ phương trình:
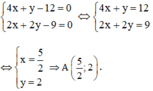
B là giao điểm BH và AB nên tọa độ điểm B là nghiệm của hệ:
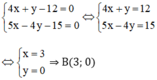
+ AC ⊥ HB, mà HB có một vtpt là (5; -4)⇒ AC nhận (4; 5) là một vtpt
AC đi qua 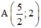
⇒ Phương trình đường thẳng AC: 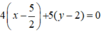 hay 4x + 5y – 20 = 0.
hay 4x + 5y – 20 = 0.
+ CH ⊥ AB, AB có một vtpt là (4; 1) ⇒ CH nhận (1; -4) là một vtpt
CH đi qua 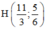
⇒ Phương trình đường thẳng CH: 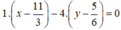 hay CH: 3x – 12y - 1 = 0.
hay CH: 3x – 12y - 1 = 0.
+ BC ⊥ AH , mà AH nhận (2; 2) là một vtpt
⇒ BC nhận (1; -1) là một vtpt
BC đi qua B(3; 0)
⇒ Phương trình đường thẳng BC: 1(x - 3) – 1(y – 0) = 0 hay x – y – 3 = 0.

gọi 3 ngăn cần tìm là a,b,c ta có
a/5=b/6 và b/8=c/9\(\dfrac{ }{ }\)
⇒a/20=b/24=c/27⇒a/20=b/24=c/27=\(\dfrac{c-a}{27-20}\) =14/7=2
⇒a=2.20=40
⇒b=2.24=48
⇒c=2.27=54
A B C A' B' C' H
Tọa độ điểm A là giao điểm của AB và AA'
\(\left\{{}\begin{matrix}4x+y-12=0\\2x+2y-9=0\end{matrix}\right.\)<=>\(\left\{{}\begin{matrix}x=2,5\\y=2\end{matrix}\right.\)
=>A(2,5;2)
Tọa độ điểm B là giao điểm của AB và BB'
\(\left\{{}\begin{matrix}4x+y-12=0\\5x-4y-15=0\end{matrix}\right.\)<=>\(\left\{{}\begin{matrix}x=3\\y=0\end{matrix}\right.\)
=>B(3;0)
AA' vuông góc với BC
=>VTCP của BC là VTPT của AA': \(\overrightarrow{n}=\left(1;1\right)\)
=>VTPT của BC là: \(\overrightarrow{n'}=\left(1;-1\right)\)và B(3;0) thuộc BC
Phương trình đường thẳng BC: 1(x-3)-1(y-0)=0
hay (BC): x-y-3=0
BB' vuông góc với AC
=>VTCP của AC là: \(\overrightarrow{m}=\left(5;-4\right)\)
=>VTPT của AC là: \(\overrightarrow{m'}=\left(4;5\right)\) và A(2,5;2) thuộc AC
=>(AC): 4(x-2,5)+5(y-2)=0
hay (AC):4x+5y-20=0
Vậy...
cho mình hỏi tại sao VTPT của AA' là (1,1) v ạ