Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
i: Độ lớn của trận động đất là;
\(M=log\left(\dfrac{A}{A_0}\right)=log\left(\dfrac{10^{5.1}\cdot A_0}{A_0}\right)=5,1\)(richter)
ii: Độ lớn của trận động đất là:
\(M=log\left(\dfrac{A}{A_0}\right)=log\left(\dfrac{65\cdot10^3\cdot A_0}{A_0}\right)=log\left(65000\right)\simeq4,81\)(richter)
b: \(A_N=3\cdot A_P\)
\(M_N=log\left(\dfrac{A_N}{A_0}\right);M_P=log\left(\dfrac{A_P}{A_0}\right)\)
\(M_N-M_P=log\left(\dfrac{A_N}{A_0}\right)-log\left(\dfrac{A_P}{A_0}\right)\)
\(=log\left(\dfrac{A_N}{A_P}\right)=log3\simeq0,48\)
=>Trận động đất ở địa điểm N lớn hơn 0,48 độ richter

a: Khi \(A=10^{3.5}\mu m\) thì M=3,5
Khi \(A=100000\mu m\) thì M=5
Khi \(A=100\cdot10^{4.3}=10^{6.3}\mu m\) thì M=6,3
b: Nó phải thỏa mãn hệ thức \(10^M=65000\)

a) Tại thời điểm t = 2 độ sâu của nước là: \(h\left( 2 \right) = 0,8cos0,5.2 + 4 \approx 4,43{\rm{ }}m.\)
Vậy độ sâu của nước ở thời điểm t = 2 là khoảng 4,43 m.
b) Các thời điểm để mực nước sâu là 3,6m tương ứng với phương trình \(0,8cos0,5t + 4 = 3,6\).
Ta có: \(0,8cos0,5t + 4 = 3,6\)
\(\begin{array}{l} \Leftrightarrow cos0,5t = - \frac{1}{2} = cos\frac{{2\pi }}{3}\\ \Leftrightarrow 0,5t = \pm \frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}\\ \Leftrightarrow t = \pm \frac{{4\pi }}{3} + k4\pi ,k \in \mathbb{Z}\end{array}\)
Với \(t = \frac{{4\pi }}{3} + k4\pi \), trong 12 tiếng ta có các thời điểm \(0 \le \frac{{4\pi }}{3} + k4\pi \le 12 \Leftrightarrow - 0,3 \le k \le 0,62 \Rightarrow k = 0. \Rightarrow t = \frac{{4\pi }}{3}\)
Với \(t = - \frac{{4\pi }}{3} + k4\pi \), trong 12 tiếng ta có các thời điểm \(0 \le - \frac{{4\pi }}{3} + k4\pi \le 12 \Leftrightarrow 0,3 \le k \le 1,28 \Rightarrow k = 1 \Rightarrow t = - \frac{{4\pi }}{3} + 4\pi = \frac{{8\pi }}{3}\)
Vậy tại các thời điểm \(t = \frac{{4\pi }}{3}\), \(t = \frac{{8\pi }}{3}\) giờ thì tàu có thể hạ thủy.

tham khảo:
Tháp lớn tại Bảo tàng Louvre ở Paris có dạng hình chóp với các cạnh bên bằng nhau nên hình chiếu của đỉnh trên đáy tháp sẽ cách đều 4 đỉnh ở đáy mà đáy là hình vuông do đó hình chiếu của đỉnh là tâm của đáy tháp.

Tham khảo:
a) 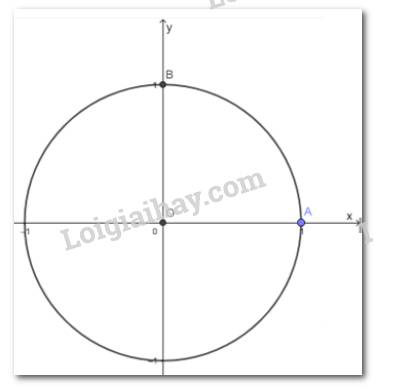
Góc lượng giác \(\left( {OA;OB} \right) = 90^\circ = \frac{\pi }{2}\)
b)

Hàm số \(F\left( r \right)\) có tập xác định là \(\left( {0; + \infty } \right)\).
Hàm số \(F\left( r \right)\) xác định trên từng khoảng \(\left( {0;R} \right)\) và \(\left( {R; + \infty } \right)\) nên hàm số liên tục trên các khoảng đó.
Ta có: \(F\left( R \right) = \frac{{GM}}{{{R^2}}}\)
\(\begin{array}{l}\mathop {\lim }\limits_{r \to {R^ + }} F\left( r \right) = \mathop {\lim }\limits_{r \to {R^ + }} \frac{{GM}}{{{r^2}}} = \frac{{GM}}{{{R^2}}}\\\mathop {\lim }\limits_{r \to {R^ - }} F\left( r \right) = \mathop {\lim }\limits_{r \to {R^ - }} \frac{{GMr}}{{{R^3}}} = \frac{{GMR}}{{{R^3}}} = \frac{{GM}}{{{R^2}}}\end{array}\)
Vì \(\mathop {\lim }\limits_{r \to {R^ + }} F\left( r \right) = \mathop {\lim }\limits_{r \to {R^ - }} F\left( r \right) = \frac{{GM}}{R}\) nên \(\mathop {\lim }\limits_{r \to R} F\left( r \right) = \frac{{GM}}{R} = F\left( R \right)\).
Vậy hàm số \(F\left( r \right)\) liên tục tại điểm \({r_0} = R\).
Vậy hàm số \(F\left( r \right)\) liên tục trên \(\left( {0; + \infty } \right)\).

a) Chiều dài một vòng của quỹ đạo là : \(9000.2.\pi \) (km)
Quãng đường vệ tinh đã chuyển động được sau 1 giờ là \(\frac{{9000.2.\pi }}{3} = 6000\pi \)(km)
Quãng đường vệ tinh đã chuyển động được sau 3 giờ là \(18000\pi \)(km)
Quãng đường vệ tinh đã chuyển động được sau 5 giờ là \(\frac{{9000.2.\pi }}{3}.5 = 30000\pi \)(km)
b)Vệ tinh chuyển động được quãng đường 200 000 km sau sô giờ là : \(\frac{{200000}}{{6000\pi }} \approx 11\)(giờ)

a, Độ cao của máy bay khi áp suất không khí ngoài máy bay bằng \(\dfrac{1}{2}P_0\) là:
\(h=-19,4\cdot log\dfrac{\dfrac{1}{2}P_0}{P_0}=-10,4\cdot log\dfrac{1}{2}\approx5,84\left(km\right)\)
b, Độ cao của ngọn núi A là: \(h_A=-19,4\cdot log\dfrac{P_A}{P_0}\)
Độ cao của ngọn núi B là: \(h_B=-19,4\cdot log\dfrac{P_B}{P_0}\)
Áp suất không khí tại đỉnh của ngọn núi A bằng \(\dfrac{4}{5}\) lần áp suất không khí tại đỉnh của ngọn núi B nên ta có: \(P_A=\dfrac{4}{5}P_B\Rightarrow\dfrac{P_A}{P_B}=\dfrac{4}{5}\)
Ta có:
\(h_A-h_B=\left(-19,4\cdot log\dfrac{P_A}{P_0}\right)-\left(-19,4\cdot log\dfrac{P_B}{P_0}\right)\\ =-19,4\cdot log\dfrac{P_A}{P_0}+19,4\cdot log\dfrac{P_B}{P_0}\\ =-19,4\cdot log\dfrac{P_A}{P_B}\\ =-19,4\cdot log\dfrac{4}{5}\approx1,88\left(km\right)\)
Vậy ngọn núi A cao hơn ngọn núi B 1,88km.

a) Tính xấp xỉ năng lượng giải toả tại tâm địa chấn ở 5 độ Richter:
Thay M = 5 vào công thức, ta có:
\(logE\approx11,4+1,5.5\approx18,9\\ \Rightarrow E\approx10^{18,9}\)
b) Tính tỷ lệ năng lượng giải toả tại tâm địa chấn ở 8 độ Richter so với tại tâm địa chấn ở 5 độ Richter:
\(logE\approx11,4+1,5.8\approx23,4\\ \Rightarrow E\approx10^{23,4}\)
`=>` Gấp khoảng 31623 lần