Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
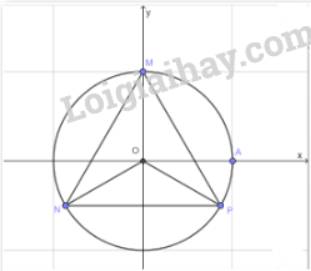
\(\begin{array}{l}(OM,ON) = (OA,ON) - (OA,OM) = \frac{{2\pi }}{3}\\ \Rightarrow \widehat {MON} = {120^0}\\\widehat {MOP} = \widehat {MOA} + \widehat {AOP} = {90^0} + {30^0} = {120^0}\\ \Rightarrow \widehat {NOP} = {360^0} - {120^0} - {120^0} = {120^0}\end{array}\)
Cung MP = cung NP = cung NM
\(\Rightarrow MP = NP = NM\)
\(\Rightarrow \Delta MNP\) đều

Tham khảo:
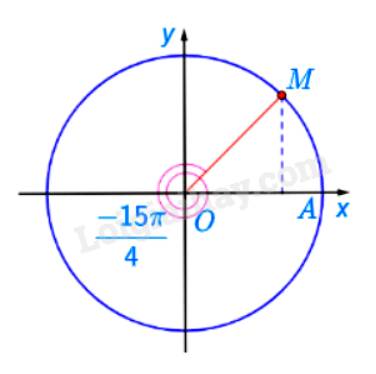
Điểm biểu diễn góc lượng giác có số đo bằng \( - \frac{{15\pi }}{4} = - \frac{{7\pi }}{4} + ( - 1).2\pi \) được xác định là điểm M.
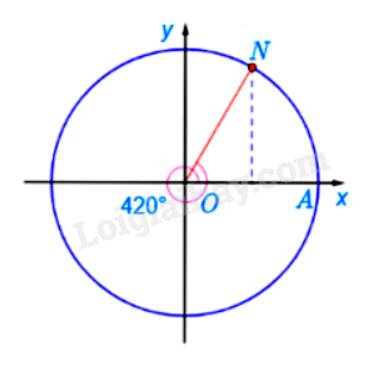
Ta có \(\frac{{420}}{{360}} = 1+ \frac{1}{6}\) Ta chia đường tròn thành 6 phần bằng nhau. Khi đó điểm N là điểm biểu diễn bởi góc có số đo \({420^ \circ }\)

Đáp án B.
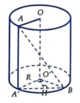
Kẻ ![]()
Vẽ O'H ⊥ A'B thì H là trung điểm của A'B.
∆ O'A'H vuông tại H nên
![]()
![]()
![]()
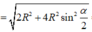
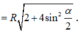

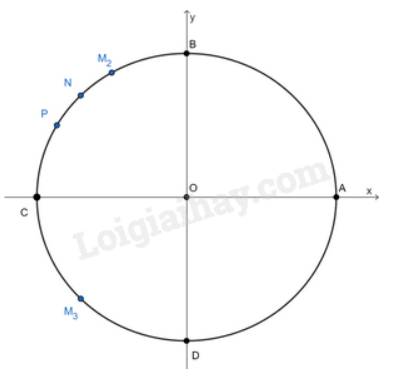
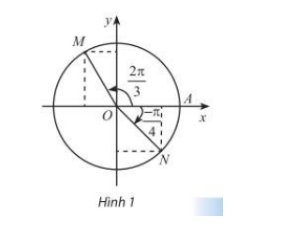
a) Ta có: \(\frac{{\frac{{2\pi }}{3}}}{{2\pi }} = \frac{1}{3}\). Ta chia đường tròn thành 3 phần bằng nhau. Khi đó điểm \({M_2}\) là điểm biểu diễn bởi góc có số đo \(\frac{{2\pi }}{3}\).
b) Ta có \( - \frac{{11\pi }}{4} = - \frac{{3\pi }}{4} + \left( { - 1} \right).2\pi \). Do đó điểm biểu diễn bởi góc \( - \frac{{11\pi }}{4}\) trùng với góc \( - \frac{{3\pi }}{4}\) và là điểm \({M_3}\).
c) Ta có \(\frac{{150}}{{180}} = \frac{5}{6}\). Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó P là điểm biểu diễn bởi góc \({150^0}\)
d) Ta có \( - {225^0} = - {180^0} - {45^0}\). Do đó điểm biểu diễn N là điểm biểu diễn bởi góc \( - {225^0}\)

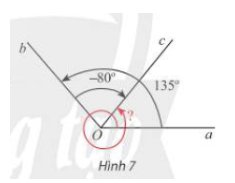
a, Số đo của góc lượng giác (Oa, Ob) trong Hình 7 là \(135^o+n\cdot360^o,n\in Z\)
Số đo của góc lượng giác (Oa, Ob) trong Hình 7 là \(-80^o+m\cdot360^o,m\in Z\)
Số đo của góc lượng giác (Oa, Ob) trong Hình 7 là \(415^o+k\cdot360^o,k\in Z\)
b, \(\left(Oa,Ob\right)+\left(Ob,Oc\right)=135^o+n\cdot360^o+\left(-80^o\right)+m\cdot360^o\\ =55^o+\left(n+m\right)\cdot360^o\\ =415^o+\left(n+m-1\right)\cdot360^o\\ =415^o+k\cdot360^o=\left(Oa,Oc\right)\)
Với \(k=n+m-1;n,m,k\in Z\)

Tham khảo:
a) Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó điểm M là điểm biểu diễn bởi góc có số đo \(\frac{{5\pi }}{6}\)
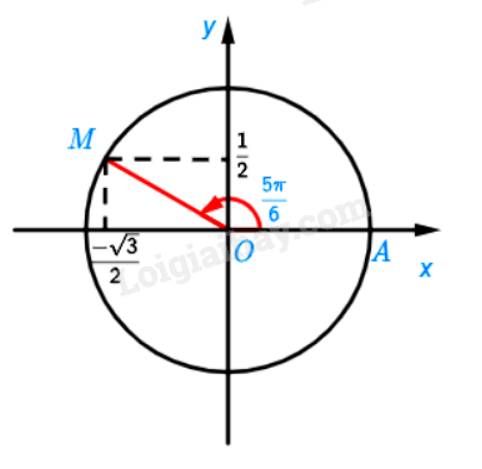
b) Ta có:
\(\sin \left( {\frac{{5\pi }}{6}} \right) = \frac{1}{2};\cos \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{2};\tan \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{3};\cot \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - 3}}{{\sqrt 3 }}\)

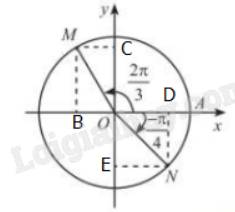
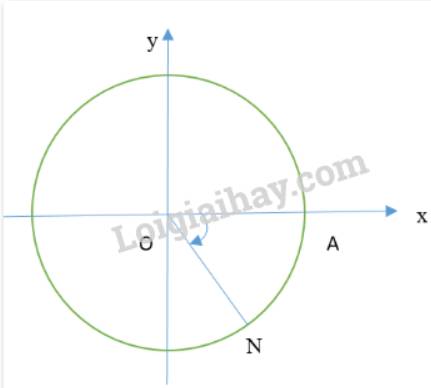
Gọi B, C lần lượt là hình chiếu của M lên Ox, Oy; D, E lần lượt là hình chiếu của N lên Ox, Oy
Ta có: OM = ON = 1
\(\widehat{MOC}=\dfrac{2\pi}{3}-\dfrac{\pi}{2}=\dfrac{\pi}{6}\\ \Rightarrow\left\{{}\begin{matrix}sin\widehat{MOC}=\dfrac{1}{2}\Rightarrow MC=\dfrac{1}{2}\\cos\widehat{MOC}=\dfrac{\sqrt{3}}{2}\Rightarrow MB=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
Do điểm M có hoành độ nằm bên trái trục Ox nên tọa độ của điểm M là \(M\left(-\dfrac{1}{2};\dfrac{\sqrt{3}}{2}\right)\)
\(\widehat{NOD}=-\dfrac{\pi}{4}\\ \Rightarrow\left\{{}\begin{matrix}sin\widehat{NOD}=-\dfrac{\sqrt{2}}{2}\Rightarrow ND=-\dfrac{\sqrt{2}}{2}\\cos\widehat{NOD}=\dfrac{\sqrt{2}}{2}\Rightarrow NE=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
Vậy tọa độ điểm N là \(N\left(\dfrac{\sqrt{2}}{2};-\dfrac{\sqrt{2}}{2}\right)\)

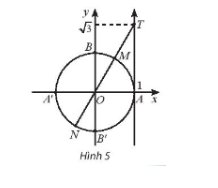
Những điểm biểu diễn góc x trên đường tròn lượng giác có \(tanx = \sqrt 3 \) là M và N.
Điểm M là điểm biểu diễn các góc lượng giác có số đo \(\frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\).
Điểm N là điểm biểu diễn các góc lượng giác có số đo \( - \frac{{2\pi }}{3} + k\pi ,k \in \mathbb{Z}\).
Tham khảo:
a)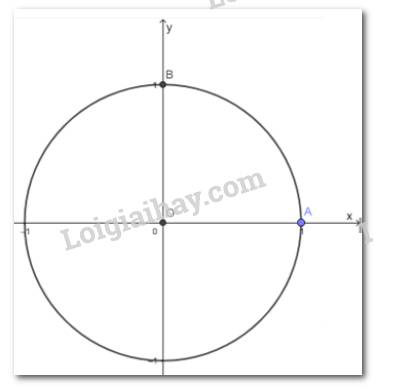
Góc lượng giác \(\left( {OA;OB} \right) = 90^\circ = \frac{\pi }{2}\)
b)