Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

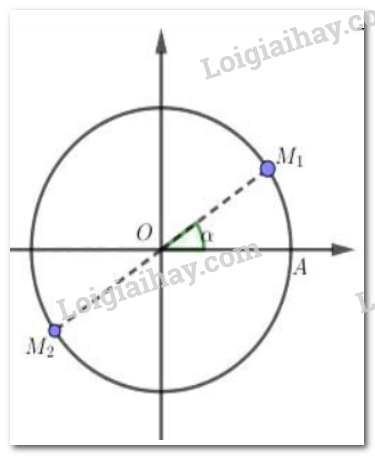
a) Hoành độ của điểm M và M’ bằng nhau
Tung độ của điểm M và M’ đối nhau
b) Mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác \(\alpha \,\,v\`a \,\, - \alpha \)


+ Xét góc lượng giác \(\frac{\pi }{2} + k\frac{{2\pi }}{3}\)
Với k = 0 thì \(\frac{\pi }{2} + 0.\frac{{2\pi }}{3} =\frac{\pi }{2} \) được biểu diễn bởi điểm B.
Với k = 1 thì \(\frac{\pi }{2} + 1.\frac{{2\pi }}{3} =\frac{7\pi }{6} \) được biểu diễn bởi điểm C.
Với k = 2 thì \(\frac{\pi }{2} + 2.\frac{{2\pi }}{3} =\frac{11\pi }{6} \) được biểu diễn bởi điểm D.
+ Xét góc lượng giác \(\frac{\pi }{2} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\)
Với k = 0 thì \(\frac{\pi }{2} + 0.\frac{{\pi }}{3} =\frac{\pi }{2} \) được biểu diễn bởi điểm B.
Với k = 1 thì \(\frac{\pi }{2} + 1.\frac{{\pi }}{3} =\frac{5\pi }{6} \) không biểu diễn bởi điểm nào.
+ Xét góc lượng giác \(\frac{{ - \pi }}{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\)
Với k = 1 thì \(\frac{{ - \pi }}{6}+ 1.\frac{{2\pi }}{3} =\frac{\pi }{2} \) được biểu diễn bởi điểm B.
Với k = 2 thì \(\frac{{ - \pi }}{6}+ 2.\frac{{2\pi }}{3} =\frac{7\pi }{6} \) được biểu diễn bởi điểm C.
Với k = 3 thì \(\frac{{ - \pi }}{6} + 3.\frac{{2\pi }}{3} =\frac{11\pi }{6} \) được biểu diễn bởi điểm D.
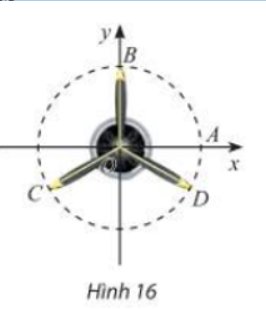
Vậy các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể được biểu diễn cho các góc lượng giác
\(\frac{\pi }{2} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right);\frac{{ - \pi }}{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\,\,\left( {k \in \mathbb{Z}} \right)\)

Tham khảo:
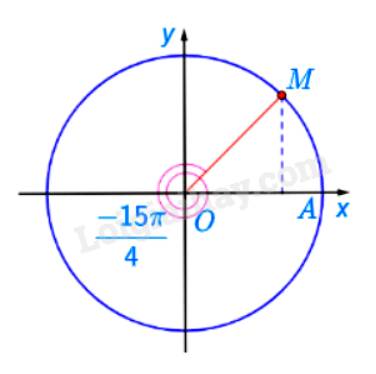
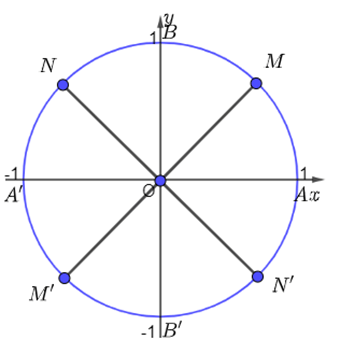
Điểm biểu diễn góc lượng giác có số đo bằng \( - \frac{{15\pi }}{4} = - \frac{{7\pi }}{4} + ( - 1).2\pi \) được xác định là điểm M.
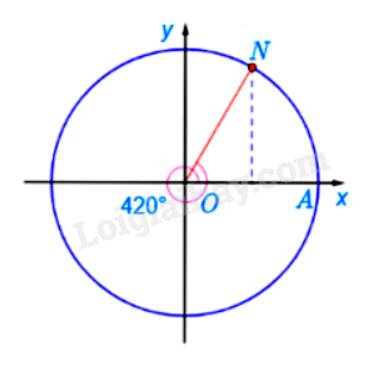
Ta có \(\frac{{420}}{{360}} = 1+ \frac{1}{6}\) Ta chia đường tròn thành 6 phần bằng nhau. Khi đó điểm N là điểm biểu diễn bởi góc có số đo \({420^ \circ }\)

Tham khảo:
a) Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó điểm M là điểm biểu diễn bởi góc có số đo \(\frac{{5\pi }}{6}\)
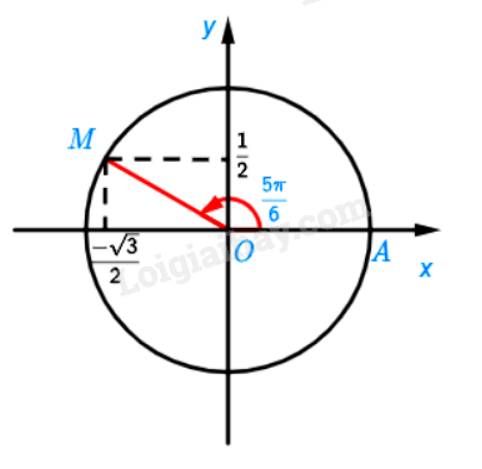
b) Ta có:
\(\sin \left( {\frac{{5\pi }}{6}} \right) = \frac{1}{2};\cos \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{2};\tan \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{3};\cot \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - 3}}{{\sqrt 3 }}\)

Giả sử số đo ba góc của tam giác lần lượt là \({u_1};{u_1}.2 = 2{u_1};{u_1}{.2^2} = 4{u_1}\left( {{u_1} > 0} \right)\).
Tổng số đo ba góc của một tam giác bằng \(\pi \) nên ta có phương trình:
\({u_1} + 2{u_1} + 4{u_1} = \pi \Leftrightarrow 7{u_1} = \pi \Leftrightarrow {u_1} = \frac{\pi }{7}\)
Vậy số đo các góc của tam giác đó lần lượt là: \(\frac{\pi }{7};\frac{{2\pi }}{7};\frac{{4\pi }}{7}\).
Chọn D.

a)
\(\begin{array}{l}\cos \left( {\frac{\pi }{3} + k2\pi \,} \right) = \cos \left( {\frac{\pi }{3}} \right) = \frac{1}{2}\\\sin \left( {\frac{\pi }{3} + k2\pi \,} \right) = \sin \left( {\frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2}\\\tan \left( {\frac{\pi }{3} + k2\pi \,} \right) = \frac{{\sin \left( {\frac{\pi }{3} + k2\pi \,\,} \right)}}{{\cos \left( {\frac{\pi }{3} + k2\pi \,\,} \right)}} = \sqrt 3 \\\cot \left( {\frac{\pi }{3} + k2\pi \,\,} \right) = \frac{1}{{\tan \left( {\frac{\pi }{3} + k2\pi \,\,} \right)}} = \frac{{\sqrt 3 }}{3}\end{array}\)
b) Các giá trị lượng giác của góc lượng giác \(\frac{\pi }{3}+\left( 2k+1 \right)\pi \,\,\left( k\in \mathbb{Z} \right)\)
$ \cos \left[\frac{\pi}{3}+(2 \mathrm{k}+1) \pi\right]=\cos \left(\frac{\pi}{3}+\pi+2 \mathrm{k} \pi\right)=\cos \left(\frac{\pi}{3}+\pi\right)=-\cos \frac{\pi}{3}=-\frac{1}{2}$
$\sin \left[\frac{\pi}{3}+(2 \mathrm{k}+1) \pi\right]=\sin \left(\frac{\pi}{3}+\pi+2 \mathrm{k} \pi\right)=\sin \left(\frac{\pi}{3}+\pi\right)=-\sin \frac{\pi}{3}=-\frac{\sqrt{3}}{2}$
$\tan \left[\frac{\pi}{3}+(2 \mathrm{k}+1) \pi\right]=\tan \frac{\pi}{3}=\sqrt{3}$;
$\tan \left[\frac{\pi}{3}+(2 \mathrm{k}+1) \pi\right]=\cot \frac{\pi}{3}=\frac{\sqrt{3}}{3}$
c)
\(\begin{array}{l}\cos \left( {k\pi \,} \right) = \left[ \begin{array}{l} - 1\,\,\,\,\,\,\,\,\,\,\,\,\,;k = 2n + 1\\1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,;k = 2n\,\,\,\end{array} \right.\\\sin \left( {k\pi \,} \right) = 0\\\tan \left( {k\pi \,} \right) = \frac{{\sin \left( {k\pi \,\,} \right)}}{{\cos \left( {k\pi \,\,} \right)}} = 0\\\cot \left( {k\pi \,\,} \right)\end{array}\)
d)
\(\begin{array}{l}\cos \left( {\frac{\pi }{2} + k\pi \,} \right) = 0\\\sin \left( {\frac{\pi }{2} + k\pi \,} \right) = \left[ \begin{array}{l}\sin \left( { - \frac{\pi }{2}} \right)\, = - 1\,\,\,\,\,\,\,;k = 2n + 1\\\sin \left( {\frac{\pi }{2}\,} \right)\, = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,;k = 2n\,\,\,\end{array} \right.\\\tan \left( {\frac{\pi }{2} + k\pi \,} \right)\\\cot \left( {\frac{\pi }{2} + k\pi \,\,} \right) = 0\end{array}\)

a) Vì \(\sin \frac{\pi }{6} = \frac{1}{2}\) nên ta có phương trình \(sin2x = \sin \frac{\pi }{6}\)
\( \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{6} + k2\pi \\2x = \pi - \frac{\pi }{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{12}} + k\pi \\x = \frac{{5\pi }}{{12}} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
\(\begin{array}{l}b,\,\,sin(x - \frac{\pi }{7}) = sin\frac{{2\pi }}{7}\\ \Leftrightarrow \left[ \begin{array}{l}x - \frac{\pi }{7} = \frac{{2\pi }}{7} + k2\pi \\x - \frac{\pi }{7} = \pi - \frac{{2\pi }}{7} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{3\pi }}{7} + k2\pi \\x = \frac{{6\pi }}{7} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
\(\begin{array}{l}\;c)\;sin4x - cos\left( {x + \frac{\pi }{6}} \right) = 0\\ \Leftrightarrow sin4x = cos\left( {x + \frac{\pi }{6}} \right)\\ \Leftrightarrow sin4x = \sin \left( {\frac{\pi }{2} - x - \frac{\pi }{6}} \right)\\ \Leftrightarrow sin4x = \sin \left( {\frac{\pi }{3} - x} \right)\\ \Leftrightarrow \left[ \begin{array}{l}4x = \frac{\pi }{3} - x + k2\pi \\4x = \pi - \frac{\pi }{3} + x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{15}} + k\frac{{2\pi }}{5}\\x = \frac{{2\pi }}{9} + k\frac{{2\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
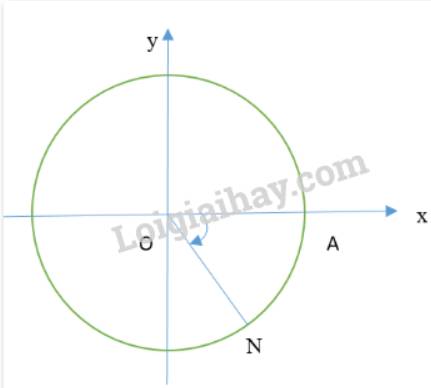

Tham khảo:
\(\begin{array}{l}(OM,ON) = (OA,ON) - (OA,OM) = \frac{{2\pi }}{3}\\ \Rightarrow \widehat {MON} = {120^0}\\\widehat {MOP} = \widehat {MOA} + \widehat {AOP} = {90^0} + {30^0} = {120^0}\\ \Rightarrow \widehat {NOP} = {360^0} - {120^0} - {120^0} = {120^0}\end{array}\)
Cung MP = cung NP = cung NM
\(\Rightarrow MP = NP = NM\)
\(\Rightarrow \Delta MNP\) đều