Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kéo dài đường cao AH lần lượt cắt BC và đường tròn ngoại tiếp tam giác ABC tại hai điển E và K, ta dễ dàng chứng minh được E là trung điểm HK
Đường cao \(AH\perp BC\) nên có phương trình \(x-y=0\), E là giao điểm của BC và AH \(\Rightarrow E\left(4;4\right)\) và H là trung điểm \(HK\Rightarrow K\left(3;3\right)\), suy ra bán kính đường tròn ngoại tiếp tam giác ABC là \(R=IK=\sqrt{5}\)
\(\Rightarrow\) phương trình đường tròn là \(\left(x-5\right)^2+\left(y-4\right)^2=5,\left(C\right)\)
Vậy hai điểm B, C là nghiệm của hệ hai phương trình đường thẳng BC và đường tròn (C) \(\Rightarrow B\left(3;5\right);C\left(6;2\right)\) và đỉnh A là nghiệm hệ của đường cao AH và đường tròn (C) \(\Rightarrow A\left(6;6\right)\)
Diện tích tam giác ABC là :
\(S_{ABC}=\frac{1}{2}d\left(A,BC\right).BC=\frac{1}{2}\frac{\left|6+6-8\right|}{\sqrt{2}}.3\sqrt{2}=6\)

Gọi \(I=AM\cap BN\), \(\Delta BIM\) đồng dạng \(\Delta ABM\)
suy ra \(AM\perp BN\) nên \(BN:-2x-y+c=0\)
\(N\left(0;-2\right)\Rightarrow c=-2\Rightarrow BN:2x-y-2=0\)
Tọa độ điểm I là nghiệm hệ phương trình :
\(\begin{cases}x+2y-2=0\\2x-y-2=0\end{cases}\)\(\Leftrightarrow\begin{cases}x=\frac{6}{5}\\y=\frac{2}{5}\end{cases}\) \(\Rightarrow I\left(\frac{6}{5};\frac{2}{5}\right)\)
Từ \(\Delta ABM\) vuông : \(BI=\frac{AB.BM}{\sqrt{AB^2+BM^2}}=\frac{4}{\sqrt{5}}\)
Tọa độ điểm \(B\left(x;y\right)\) thỏa mãn \(\begin{cases}B\in BN\\BI=\frac{4}{\sqrt{5}}\end{cases}\) \(\Rightarrow\begin{cases}2x-y-2=0\\\left(\frac{6}{5}-x\right)^2+\left(\frac{2}{5}-y\right)^2=\frac{16}{5}\end{cases}\)
Giải hệ ta được \(\begin{cases}x=2\\y=2\end{cases}\) và \(\begin{cases}x=\frac{2}{5}\\y=\frac{-6}{5}\end{cases}\) Suy ra \(B\left(2;2\right)\) Loại \(\left(\frac{2}{5};-\frac{6}{5}\right)\)
Tọa đọ M(x;y) thỏa mãn \(\begin{cases}M\in AM\\IM=\sqrt{BM^2-BI^2}\end{cases}\) \(\Rightarrow\begin{cases}x+2y-2=0\\\left(x-\frac{6}{5}\right)^2+\left(y-\frac{2}{5}\right)^2=\frac{4}{5}\end{cases}\)
Giải hệ ta được : \(\begin{cases}x=2\\y=0\end{cases}\) và \(\begin{cases}x=\frac{2}{5}\\y=\frac{4}{5}\end{cases}\) suy ra \(M_1\left(2;0\right);M_2\left(\frac{2}{5};\frac{4}{5}\right)\)

C K O E H F B A D
Trên \(\Delta\) lấy điểm D sao cho à D, A nằm khác phía nhau so với B. Gọi E là giao điểm của các đường thẳng KA và OC; Gọi F là giao điểm của các đường thẳng KB và OD
Vì K là tâm đường tròn bàng tiếp góc O của tam giác OAB nên KE là phân giác của góc OAC. Mà OAC là tam giác cân tại A ( do OA = AC, theo gt) nên suy ra KE cũng là đường trung trục của OC. Do đó, E là trung điểm của OC và KC=KO
Xét tương tự đối với KF, ta cũng có F là trung điểm của OD và KD=KO
Suy ra tam giác CKD cân tại K. Do đó, hạ KH vuông góc với \(\Delta\) , ta có H là trung điểm của CD. Như vậy :
+ A là giao của \(\Delta\) và đường trung trực \(d_1\) của đoạn OC (1)
+ B là giao của \(\Delta\) và đường trung trực \(d_2\) của đoạn OD, với D là điểm đối xứng của C qua H là hình chiếu vuông góc của K trên \(\Delta\) (2)
Vì \(C\in\Delta\) và có hoành độ \(x_0=\frac{24}{5}\) nên gọi \(y_0\) là tung độ của C, ta có :
\(2.\frac{24}{5}+3y_0-12=0\) suy ra \(y_0=-\frac{12}{5}\)
Từ đó, trung điểm E của OC có tọa độ là \(\left(\frac{12}{5};-\frac{6}{5}\right)\) và đường thẳng OC có phương trình \(x+2y=0\)
Suy ra phương trình của \(d_1\) là \(2x-y-6=0\)
Do đó, theo (1), tọa độ của A là nghiệm của hệ phương trình :
\(\begin{cases}4x+3y-12=0\\2x-y-6=0\end{cases}\)
Giải hệ ta có \(A=\left(3;0\right)\)
Để tìm tọa độ đỉnh B ta làm như sau :
Gọi d là đường thẳng đi qua K(6;6) và vuông góc với \(\Delta\).
Ta có phương trình của d là : \(3x-4y+6=0\). Từ đây, do H là giao điểm của \(\Delta\). và d nên tọa độ của H là nghiệm của hệ phương trình :
\(\begin{cases}4x+3y-12=0\\3x-4y+6=0\end{cases}\)
Giải hệ trên, ta được \(H=\left(\frac{6}{5};\frac{12}{5}\right)\) suy ta \(D=\left(-\frac{12}{5};\frac{26}{5}\right)\)
Do đó, trung điểm F của OD có tọa độ là \(\left(-\frac{6}{5};\frac{18}{5}\right)\) và đường thẳng OD có phương trình \(3x+y=0\)
Suy ra phương trình của \(d_2\) là \(x-3y+12=0\)
Do đó, theo (2), tọa độ B là nghiệm của hệ phương trình :
\(\begin{cases}4x+3y-12=0\\x-3y+12=0\end{cases}\)
Giải hệ trên ta được B=(0;4)






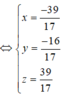



A B C D M H K N E
Gọi \(E=BN\cap AD\Rightarrow D\) là trung điểm của AE.
Dựng \(AH\perp BN\) tại H \(\Rightarrow AH=d\left(A;BN\right)=\frac{8}{\sqrt{5}}\)
Trong tam giác vuông ABE : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AE^2}=\frac{5}{4AB^2}\Rightarrow AB=\frac{\sqrt{5}.AH}{2}=4\)
\(B\in BN\Rightarrow B\left(b;8-2b\right)\left(b>2\right)\)
\(AB=4\Rightarrow B\left(3;2\right)\)
Phương trình AE : \(x+1=0\)
\(E=AE\cap BN\Rightarrow E\left(-1;10\right)\Rightarrow D\left(-1;6\right)\Rightarrow M\left(-1;4\right)\)
Gọi I là tâm của (BKM) => I là trung điểm của BM => I(1;3)
\(R=\frac{BM}{2}=\sqrt{5}\)
Vậy phương trình đường tròn : \(\left(x-1\right)^2+\left(y-3\right)^2=5\)
5