Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
=> ∆ ABC vuông tại A
Tâm I của đường tròn ngoại tiếp tam giác là trung điểm của BC, I(0;2;0)
Đường thẳng d qua tâm I và vuông góc mặt phẳng (ABC) được xác định
q u a I ( 0 ; 2 ; 0 ) V T C P : u → = 1 2 A B → , A C → = ( 3 ; - 1 ; 5 )
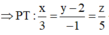
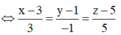
Vậy phương trình của d là x - 3 3 = y - 1 - 1 = z - 5 5
Chọn A
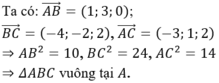
Tâm I của đường tròn ngoại tiếp tam giác là trung điểm của BC => I (0; 2; 0)
Đường thẳng d cần tìm đi qua I (0; 2; 0) và nhận vectơ 
làm véc tơ chỉ phương. Phương trình chính tắc của đường thẳng d là 
Chọn A
Ta có:
AB² = 10, BC² = 24, AC² = 14 => ∆ABC vuông tại A.
Tâm I của đường tròn ngoại tiếp tam giác là trung điểm của BC => I (0;2;0).
Đường thẳng d cần tìm đi qua I (0;2;0) và nhận vectơ 
làm véc tơ chỉ phương. Phương trình chính tắc của đường thẳng d là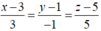 
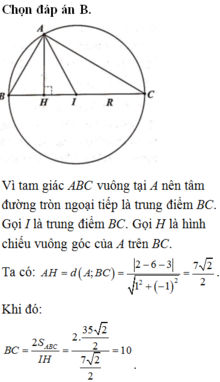
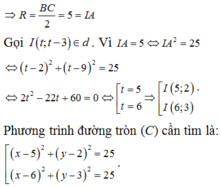
Kéo dài đường cao AH lần lượt cắt BC và đường tròn ngoại tiếp tam giác ABC tại hai điển E và K, ta dễ dàng chứng minh được E là trung điểm HK
Đường cao \(AH\perp BC\) nên có phương trình \(x-y=0\), E là giao điểm của BC và AH \(\Rightarrow E\left(4;4\right)\) và H là trung điểm \(HK\Rightarrow K\left(3;3\right)\), suy ra bán kính đường tròn ngoại tiếp tam giác ABC là \(R=IK=\sqrt{5}\)
\(\Rightarrow\) phương trình đường tròn là \(\left(x-5\right)^2+\left(y-4\right)^2=5,\left(C\right)\)
Vậy hai điểm B, C là nghiệm của hệ hai phương trình đường thẳng BC và đường tròn (C) \(\Rightarrow B\left(3;5\right);C\left(6;2\right)\) và đỉnh A là nghiệm hệ của đường cao AH và đường tròn (C) \(\Rightarrow A\left(6;6\right)\)
Diện tích tam giác ABC là :
\(S_{ABC}=\frac{1}{2}d\left(A,BC\right).BC=\frac{1}{2}\frac{\left|6+6-8\right|}{\sqrt{2}}.3\sqrt{2}=6\)