K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
1 tháng 4 2018
Trong mặt phẳng (ABCD) gọi AC giao BD tại I
Một điểm chung của hai mặt phẳng (SAC) và (SBD) khác điểm S là điểm I
I ∈ AC ⊂ (SAC)
I ∈ BD ⊂ (SBD)
FH
1

15 tháng 11 2021
Ta có: (x3 +
)8=Ck8 x3(8 – k) ()k =Ck8 x24 – 4k
Trong tổng này, số hạng Ck8 x24 – 4k không chứa x khi và chỉ khi

CM
25 tháng 3 2018
Đáp án B

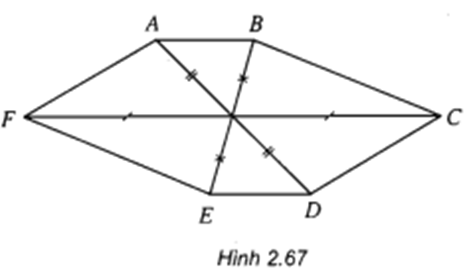
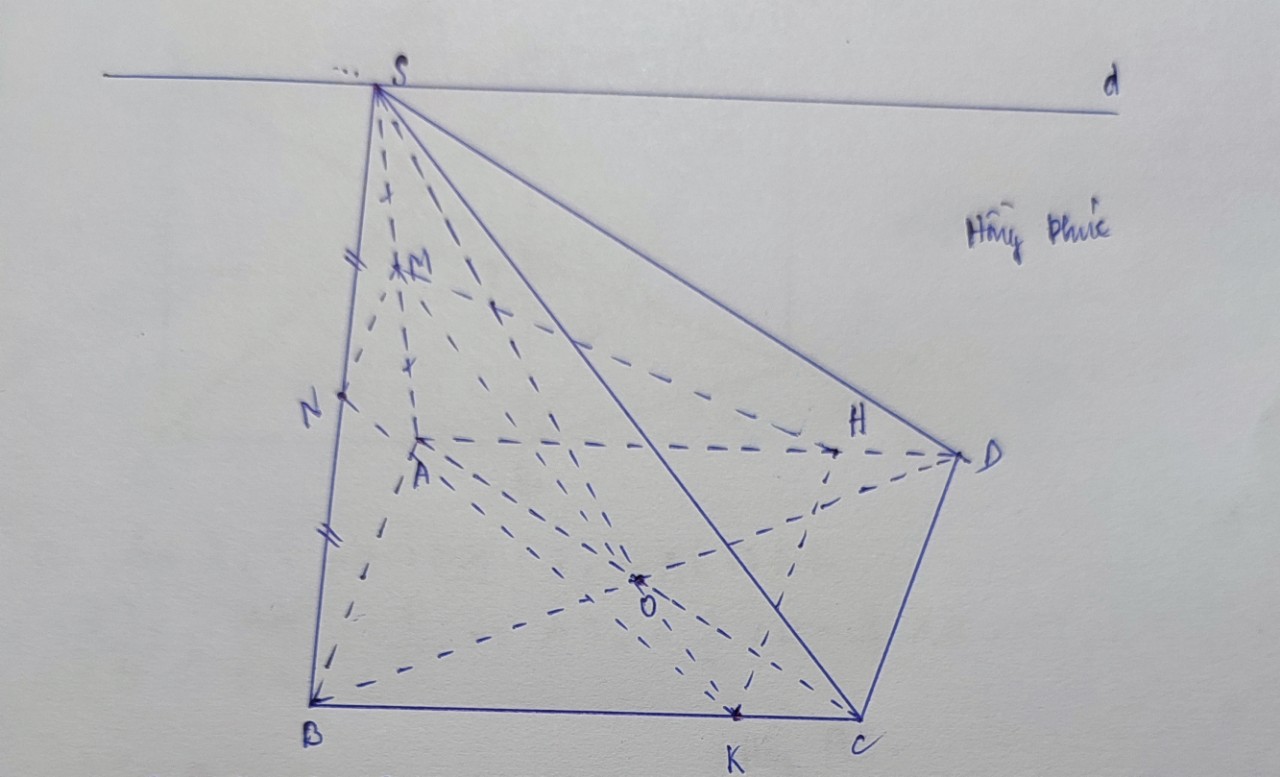
Ta có: NI ∩ SD = J

Xét (CMN) và (SAD) có:
M là điểm chung
J là điểm chung
⇒ MJ là giao tuyến của 2 mặt phẳng (CMN) và (SAD)

16 tháng 11 2021
Gọi mỗi số là abcd
d có 2 cách
a có 5 cách a#0
b có 5 cách b#a
c có 4 cách c#b,a
Nếu sai sót dì thông càm

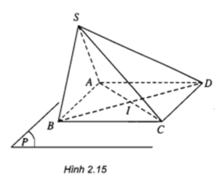
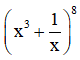
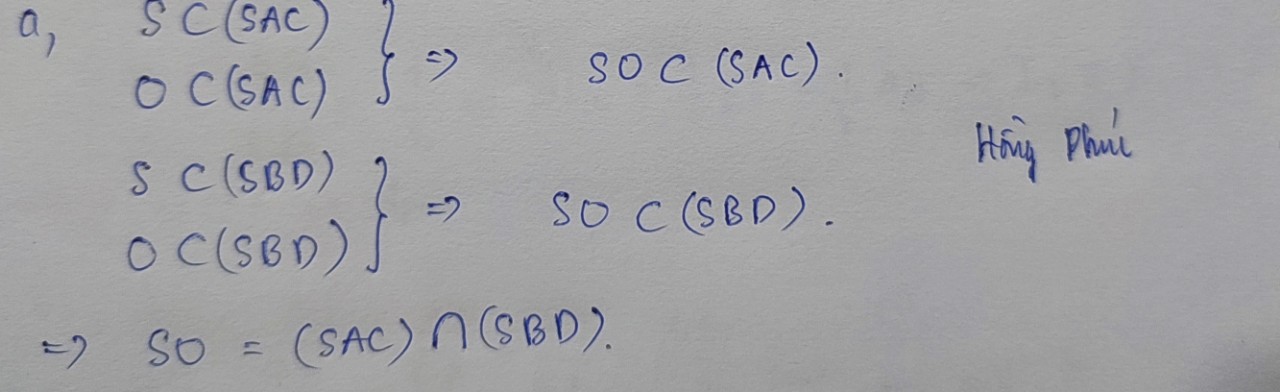
\(AC\in P;BD\in P\) => AC căt BD tại I
\(AC\in\left(SAC\right)\Rightarrow I\in\left(SAC\right)\)
\(BD\in\left(SBD\right)\Rightarrow I\in\left(SBD\right)\)
=> I là điểm chung của (SAC) và (SBD)