Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Mặt cầu (S) có tâm I (1;0;-2) và bán kính R=2.
Đường thẳng d đi qua điểm N (2; 0; m-1) và có véc tơ chỉ phương ![]()
Điều kiện để d cắt (S) tại hai điểm phân biệt là d (I; (d))<R
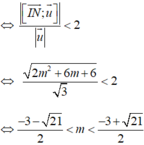
Khi đó, tiếp diện của (S) tại A và B vuông góc với IA và IB nên góc giữa chúng là góc (IA;IB).

Vậy T= {-3;0}. Tổng các phần tử của tập hợp T bằng -3.

\(\overrightarrow{OA}=\left(1;0;-1\right)\) ; \(\overrightarrow{OB}=\left(1;-1;2\right)\)
\(\Rightarrow S_{OAB}=\dfrac{1}{2}\left|\left[\overrightarrow{OA};\overrightarrow{OB}\right]\right|=\dfrac{\sqrt{11}}{2}\)

Chọn C
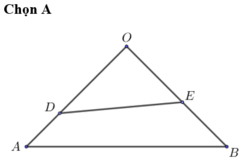
Gọi R là bán kính của mặt cầu, H là trung điểm của AB.
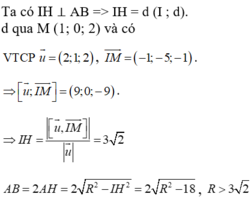
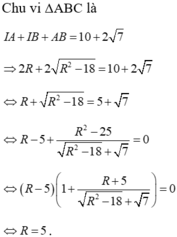
Mặt cầu (S) có tâm I (2; 5; 3), bán kính R = 5.
Phương trình mặt cầu (S) là: ![]()
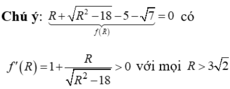
nên phương trình có nghiệm duy nhất R=5.

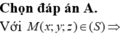
( x + 5 ) 2 + ( y + 5 ) 2 + ( z - 14 ) 2 = 324
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Dấu bằng đạt tại
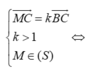
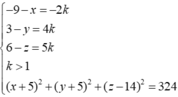

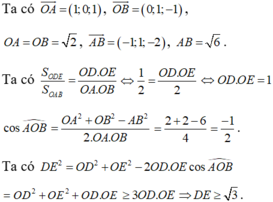
Dấu bằng xảy ra khi và chỉ khi OD = OE = 1
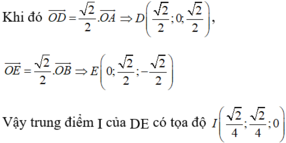
Chú ý: Sau khi chứng minh được OD=OE=1 thì ta có thể tìm trung điểm I của DE như sau: