Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

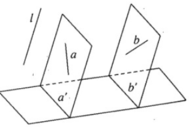
Giả sử a và b là hai đường thẳng chéo nhau có hình chiếu là a' và b'. Nếu mặt phẳng (a, a') và mặt phẳng (b, b') song song với nhau thì a′ // b′. Vậy hình chiếu song song của hai đường thẳng chéo nhau có thể song song.
Nếu a và b là hai đường thẳng cắt nhau tại O và hình chiếu của O là O' thì O′ ∈ a′ và O′ ∈ b′ tức là a' và b' có điểm chung. Vậy hình chiếu song song của hai đường thẳng cắt nhau không thể song song được.

Các mệnh đề đúng là a và d
b là mệnh đề sai vì phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau
c là mệnh đề sai vì phép chiếu song song biến tam giác đều thành một tam giác bất kì

A. Mệnh đề đảo sai (2 đường cùng mặt chưa chắc song song)
B. Sai, ví dụ 2 đường thẳng song song
C. Đúng
D. Sai, 2 đường thẳng song song (ko có quy định nào bắt 1 đường thẳng chỉ nằm trên 1 mặt)

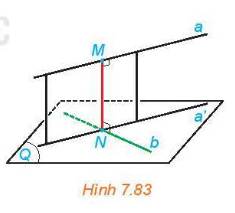
a) Mặt phẳng chứa a và a' có vuông góc với (Q)
b) Ta có \(MN \bot \left( Q \right),b \subset \left( Q \right) \Rightarrow MN \bot b\)
\(MN \bot a\) (M là hình chiếu của N trên a)
Vậy MN có vuông góc với cả hai đường thẳng a và b.
c) Vì a // (Q) nên d(a, (Q)) = d(M, (Q)) = MN

a) Sai
Sửa lại: "Đường thẳng Δ là đường thẳng vuông góc chung của hai đường thẳng chéo nhau a và b nếu Δ cắt cả a và b, đồng thời Δ ⊥ a và Δ ⊥ b"
b) Đúng
c) Đúng
d) Sai
Sửa lại: Đường thẳng đi qua M trên a và vuông góc với a, đồng thời cắt b tại N và vuông góc với b thì đó là đường vuông góc chung của a và b.
e) Sai.

Mệnh đề a,b,c đúng