Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B.
Gọi khoảng cách từ một điểm bất kỳ thuộc CD đến các nguồn A, B tương ứng là d2 và d1
Ta có 
+ Điểm cực đại trên đoạn CD thỏa mãn:
với
Có 7 giá trị của k là 
nên có 7 điểm cực đại trên CD.
+ Điểm cực tiểu trên đoạn CD thỏa mãn
,
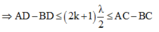
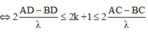
Có 6 giá trị của k thỏa mãn
nên có 6 điểm cực tiểu trên CD.
Chọn đáp án B
+ Khoảng cách ngắn nhất giữa hai điểm dao động với biên độ cực đại trên đoạn thẳng nối hai nguồn là 
Đáp án: C
HD Giải: Khoảng cách giữa hai điểm dao động với biên độ cực đại nằm trên đoạn AB cách nhau nửa bước sóng bằng 6cm
Đáp án: A
HD Giải: λ = 80 2 π 100 π = 1,6cm
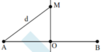
M cùng pha với nguồn A nên MA = d = (được rút ra từ phương trình sóng tại M với d1 = d2 = d)
Ta có điều kiện MA > AO = AB/2 nên
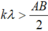
<=> 1,6k > 6
<=> k > 3,75
MA nhỏ nhất nên chọn k = 4
MA = 4.1,6 = 6,4 cm
Đáp án D
Ta có hình vẽ
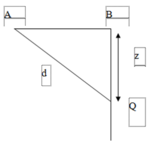
Vì hai nguồn dao động ngược pha nên ta áp dụng điều kiện để 1 điểm trong miền giao thoa dao động cực đại là:
d 1 - d 2 = ( k + 1 2 ) λ
Suy ra, điểm Q dao động cực đại khi:
d 2 + z 2 - z = ( k + 1 2 ) λ
Vì Q dao động cực đại nên điểm Q nằm trên các đường hyperbol cực đại trong miền giao thoa.
Áp dụng công thức tính số dao động cực đại trong đoạn AB:
- AB λ - 1 2 < k < AB λ - 1 2 ⇔ - 3 1 - 1 2 < k < 3 1 - 1 2
⇔ - 3 , 5 < k < 2 , 5
Vậy k nhận các giá trị : -3; +-2; +- 1; 0
Từ điều kiện Q dao động cực đại, khi Q xa nhất ứng với k = 0, thay số vào ta được:
d 2 + z 2 - z = 0 , 5 λ ⇔ 3 2 + z 2 = 0 , 5 + z
⇔ 9 + z 2 = 0 , 25 + z + z 2 ⇔ z = 8 , 75 cm .
Khi Q gần nhất ứng với k = 2 (hoặc k = -3, tùy theo bạn chọn đâu là chiều dương), thay số vào ta được:
d 2 + z 2 - z = 2 , 5 λ ⇔ 3 2 + z 2 = 2 , 5 + z
⇔ 9 + z 2 = 6 , 25 + 5 z + z 2 ⇔ z = 8 , 75
Vậy Zmin =0,55cm; Zmax = 8,75cm.
Đáp án D
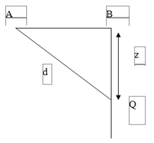
Vì hai nguồn dao động ngược pha nên ta áp dụng điều kiện để 1 điểm trong miền giao thoa dao động cực đại là: 
Suy ra, điểm Q dao động cực đại khi:
Vì Q dao động cực đại nên điểm Q nằm trên các đường hyperbol cực đại trong miền giao thoa.
Áp dụng công thức tính số dao động cực đại trong đoạn AB:
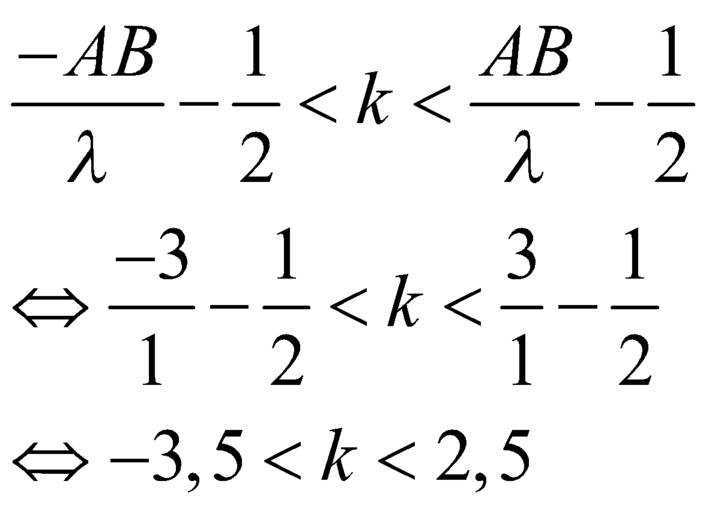
Vậy k nhận các giá trị: -3; +-2; +- 1; 0
Từ điều kiện Q dao động cực đại, khi Q xa nhất ứng với k = 0, thay số vào ta được:
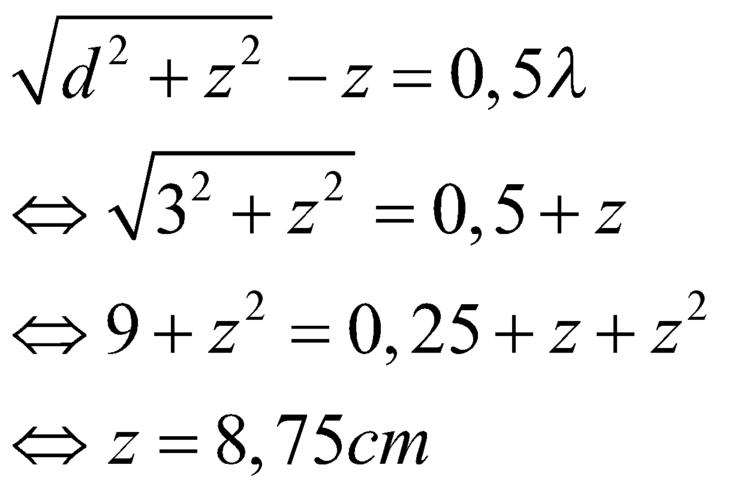
Khi Q gần nhất ứng với k = 2 (hoặc k = -3, tùy theo bạn chọn đâu là chiều dương), thay số vào ta được:
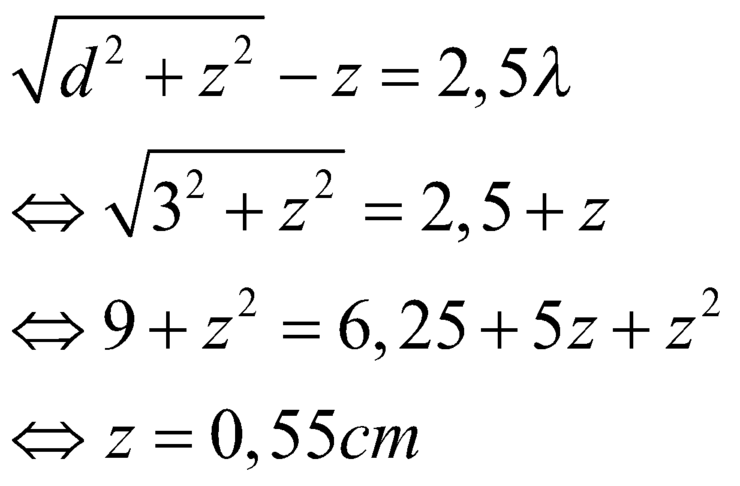
Vậy 