Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

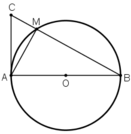
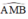 là góc nội tiếp chắn nửa đường tròn
là góc nội tiếp chắn nửa đường tròn
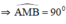
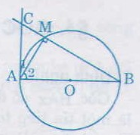
AC là tiếp tuyến của đường tròn tại A
⇒ AC ⊥ AO
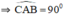
⇒ ΔABC vuông tại A có đường cao AM
⇒ AM2 = MB.MC (Hệ thức về cạnh và đường cao trong tam giác vuông).

Ta có: ∆MAB~ ∆MCA ( =
;
=
)
nên =
Suy ra MA2 = MB. MC

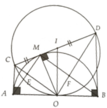
a, Dễ thấy A M B ^ = 90 0 hay E M F ^ = 90 0 tiếp tuyến CM,CA
=> OC ⊥ AM => O E M ^ = 90 0 Tương tự => O F M ^ = 90 0
Chứng minh được ∆CAO = ∆CMO => A O C ^ = M O C ^
=> OC là tia phân giác của A M O ^
Tương tự OD là tia phân giác của B O M ^ suy ra OC ⊥ OD <=> C O D ^
b, Do ∆AOM cân tại O nên OE là đường phân giác đồng thời là đường cao
=> O E M ^ = 90 0 chứng minh tương tự O F M ^ = 90 0
Vậy MEOF là hình chữ nhật
c, Gọi I là trung điểm CD thì I là tâm đường tròn đường kính CD và IO=IC=ID. Có ABDC là hình thang vuông tại A và B nên IO//AC//BD và IO vuông góc với AB. Do đó AB là tiếp tuyến của đường tròn đường kính CD.

Bài 2:
O A B C E D M
Ta thấy EB // AC nên \(\frac{EB}{MA}=\frac{ED}{DA}\Rightarrow AM.ED=EB.DA\) (1)
Do EB//AC nên \(\widehat{BCA}=\widehat{CBE}\Rightarrow\widebat{EC}=\widebat{CB}\)
Vậy thì \(2.\widehat{DMC}=\widebat{BC}-\widebat{DC}=\widebat{EC}+\widebat{EB}-\widebat{DC}=\left(\widehat{CB}-\widebat{DC}\right)+\widebat{EB}=\widebat{ED}=2.\widehat{DCE}\)
\(\Rightarrow\widehat{DMC}=\widehat{DCE}\)
Mà \(\widehat{DEC}=\widehat{DCM}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung)
\(\Rightarrow\Delta EDC\sim\Delta CDM\left(g-g\right)\Rightarrow\frac{ED}{CD}=\frac{EC}{CM}\Rightarrow CM.ED=CD.EC\) (2)
Từ (1) và (2) ta thấy, muốn chứng minh CM = MA, ta chỉ cần chứng minh EB.DA = CD.EC
Lại có \(\widebat{CE}=\widebat{CB}\Rightarrow CE=CB\)
Vậy ta cần chứng minh: EB.DA = CD.BC
Ta có \(\widehat{DAC}=\frac{\widebat{EC}-\widebat{DC}}{2}=\frac{\widebat{BC}-\widebat{DC}}{2}=\frac{\widebat{DB}}{2}=\widehat{DCB}\)
Vậy nên ta có ngay \(\Delta DBC\sim\Delta DCA\left(g-g\right)\Rightarrow\frac{BD}{CD}=\frac{BC}{CA}\Rightarrow BC.CD=BD.CA\left(3\right)\)
Ta dễ dàng thấy ngay \(\Delta BDA\sim\Delta EBA\left(g-g\right)\Rightarrow\frac{BD}{EB}=\frac{DA}{BA}=\frac{DA}{CA}\Rightarrow EB.DA=BD.CA\left(4\right)\)
Từ (3) và (4) ta có \(EB.DA=BC.CD\)
Từ đó suy ra MC = MA hay M là trung điểm của AC (đpcm).
AC là tiếp tuyến của đường tròn tại A
⇒ AC ⊥ AO
⇒ ΔABC vuông tại A có đường cao AM
⇒ (Hệ thức về cạnh và đường cao trong tam giác vuông).
Kiến thức áp dụng
+ ΔABC vuông tại A có: h2 = b’.c’
+ Góc nội tiếp chắn nửa đường tròn là góc vuông.
+ Tiếp tuyến của đường tròn (O) tại A là đường thẳng qua A và vuông góc với bán kính OA.