Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

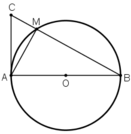
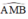 là góc nội tiếp chắn nửa đường tròn
là góc nội tiếp chắn nửa đường tròn
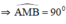
AC là tiếp tuyến của đường tròn tại A
⇒ AC ⊥ AO
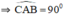
⇒ ΔABC vuông tại A có đường cao AM
⇒ AM2 = MB.MC (Hệ thức về cạnh và đường cao trong tam giác vuông).

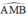 là góc nội tiếp chắn nửa đường tròn
là góc nội tiếp chắn nửa đường tròn
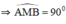
AC là tiếp tuyến của đường tròn tại A
⇒ AC ⊥ AO
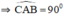
⇒ ΔABC vuông tại A có đường cao AM
⇒ (Hệ thức về cạnh và đường cao trong tam giác vuông).
Kiến thức áp dụng
+ ΔABC vuông tại A có: h2 = b’.c’
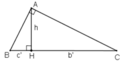
+ Góc nội tiếp chắn nửa đường tròn là góc vuông.
+ Tiếp tuyến của đường tròn (O) tại A là đường thẳng qua A và vuông góc với bán kính OA.

b) MN = AN = 1/2 AC (đường trung tuyến ứng với cạnh huyền trong tam giác AMC vuông tại M)
tam giác AON = tam giác MON (c.c.c)
=> góc OMN = 90đ hay OM vuông góc NM => NM là tiếp tuyến
c) có NM Là tiếp tuyến (câu b)
=> góc O1= góc O2 , góc O3 = góc O4 (t/c hai tiếp tuyến cắt nhau)
có O1+O2+O3+O4 = 180đ
=> O2+O3 = 90đ
=> tam giác NOD vuông tại O
Xét tam giác vuông NOD, đường cao OM
=> tam giác OMN đồng dạng với tam giác DMO
=> \(\frac{NM}{OM}=\frac{OM}{MD}\)
=>\(\frac{AN}{OM}=\frac{OM}{DB}\)
=> AN.BD=\(R^2\)
d) có AN.BD=\(R^2\)
=> 2AN . BD = 2 R.R
=>AC.BD = AB . OA
=>\(\frac{AC}{AB}=\frac{OA}{BD}\)
=> tam giác AOC đồng dạng với tam giác BDA
=>góc AOC = góc ADB
Gọi K là giao điểm của AD và OC
=> tam giác AOK đồng dạng ADB (g.g)
=>góc OKA = góc DBA = 90đ
=> \(AD\perp OC\)


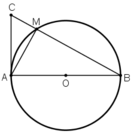
Ta có: ∆MAB~ ∆MCA (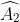 =
= 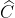 ;
; 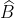 =
= 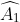 )
)
nên =
= 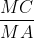
Suy ra MA2 = MB. MC